 |
Zdroje a pasívne články |
| q | Aktívny a pasívny n-bran |
Pri analýze elektronických obvodov sa používa ako stavebný kameň obvodov základný útvar - n - bran (z anglického n - port, pojem ako čierna krabička s 2n dvojicami svoriek), v najjednoduchšom prípade každá súčiastka obvodu s 2 svorkami predstavuje jednobran (podľa staršej terminológie dvojpól).
Dvojbran (napríklad delič napätia alebo prúdu, transformátor, tranzistorový zosilňovač, frekvenčný filter a pod.) je ľubovolný obvod, ktorý je spojený s inými obvodmi dvoma dvojicami svoriek:
- vstupnou dvojicou, cez ktorú energia do dvojbranu vstupuje a
- vystupnou dvojicou, cez ktorú vystupuje.
- pasívne (nedodávajú do vonkajšieho obvodu napätie alebo prúd a len ho odoberajú, t.j. správajú sa ako spotrebiče);
-
lineárne (napr. rezistor R=UR/IR,
kondenzátor C=QC/UC a pod.); Vlastnosti
lineárnych
súčiastok sú vyjadrené statickým parametrom - R, C a pod. na
rozdiel
od linearizovaných obvodov, v ktorých je V-A charakteristika nahradená
pri malých zmenách obvodových veličín DU, DI
smernicou k tejto charakteristike a hovoríme o diferencialnych
parametroch,
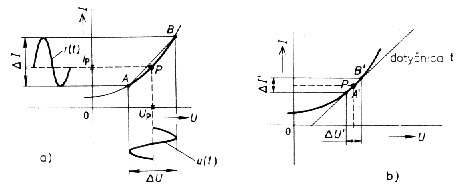
napr. r= dU/dI a pod. (resp. diferenčný parameter na obr. 1ab.)
V lineárnych obvodoch platí princíp(lineárnej) superpozície (F), na základe ktorého možno určiť výsledný účinok v obvode s viacerými zdrojmi na základe určenia reakcii od jednotlivých zdrojov, napr. prúdu a napätia alebo jednosmerného zdroja definujúceho pokojové pracovné podmienky (pracovný bod) a zdroja premenlivého signálu.);
- nelineárne (napr. dióda);
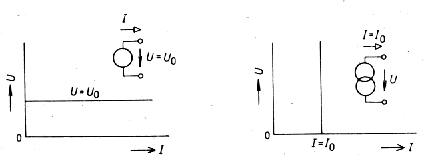
- aktívne - zdroje spravidla prijímajú neelektrickú formu energie (mechanickú, chemickú, tepelnú) a premieňajú ju na elektrickú. Jediným parametrom ideálneho zdroja napätia (obr. 1ba), je svorkové napätie u=u0(t). Jediným parametrom ideálneho zdroja prúdu (obr. 1bb), je dodávaný prúd i=i0(t).
- napätia;
- prúdu.
 |
|
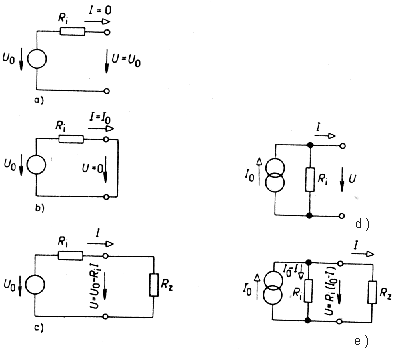
| Obr. 1a. Linearizácia charakteristiky jednobranu. a) Pracovný bod (statický a dynamický stav pri pôsobení signálu);b) diferencialny odpor v nelineárnom jednobrane. | |
 |
Obr. 1b
Voltampérová charakteristika ideálneho zdroja:
|
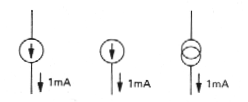
Obr. 1c. Symbolické značky zdroja napätia ako "čiernej skrinky" s dvoma svorkami. Obr. 1d. Symbolické značky zdroja prúdu 1mA.
Realne zdroje majú obmedzenú schopnosť poskytovania prúdu a napätia, takže napr. pri odbere prúdu I z reálneho zdroja napätia (zaťažovacia charakteristika na obr. 1e.) bude jeho svorkové napätieodlišné od napätia naprázdno U0 (pri odberanom prúde I).
U=U0-IRi (1)
Obr.1e.
- Zaťažovacia charakteristika skutočného zdroja.
- Sériový náhradný obvod skutočného zdroja.
Základnými charakteristickými parametrami (kvôli zjednodušeniu jednosmerných, obecne všetkých) reálnych zdrojov je :
O tom či bude obvod lepšie reprezentovať zdroj napätia (obr. 1c.) alebo zdroj prúdu (obr. 1d.) rozhodujevzťah (či je Ri<< Rz alebo Ri>>Rz) vnútorného odporu Ri a zaťažovacieho odporu Rz (obr. 1e.). Kvôli úplnosti treba dodať, že ideálny zdroj napätia má Ri =0 a ideálny zdroj prúdu 1/Ri=0 (obr. 1b.).
- napätie naprázdno (U0),
- prúd nakrátko (I0) a
- vnútorný odpor zdroja (Ri=U0/I0).
Úpravou vzťahu (1) pre Ri>>Rz možno vyjadriť vzťah pre odoberaný prúd I z prúdového zdroja (z maximálne možným prúdom - tzv. prúdom nakrátko I0, pri napätí U na svorkách zdroja.)
Reálny zdroj možno teda rovnocenne reprezentovať buď zdrojom, ktorého vlastnosti sú blizke zdoju prúdu alebo zdroju napätia.
I=U0/Ri-U/Ri=I0-U/Ri (2)
Obr. 1f
Rôzne podmienky činnosti zdroja:
- v stave naprázdno U=U0 =>(Ri=0) - je to sériový náhradný obvod skutočného zdroja;
- v stave nakrátko I=I0 =>(1/Ri=0);
- Théveninov náhradný obvod zaťažený rezistorom Rz => Medzi svorkovým napätím U, odoberaným prúdom I, napätím naprázdno U0 a vnútorným odporom Ri platí vzťah: śvorkové napätie U=U0-RiI ;
- paralelný náhradný obvod skutočného zdroja U=Ri(I0-I) ;
Nortonov náhradný obvod zaťažený rezistorom Rz => Medzi svorkovým napätím U, odoberaným prúdom I, prúdom naktátko I0 a vnútorným odporom Ri platí vzťah: śvorkové napätie U=Ri(I0-I) ;
FZákladné
metódy analýzy jednosmerných obvodov
FPrehľad
základných pojmov z teórie lineárnych elektronických obvodov
ako aj spôsobov analýzy obvodov možno získať tiež zo skrípt: P. Kohaut,
F. Kundracík : Špecialne praktikum z elektroniky I, skriptá FMFI UK,
2003
(v tvare pdf).
Príklad 1a -
ilustrácia
použitia princípu superpozície na riešenie obvodu
 |
obr. 1g.
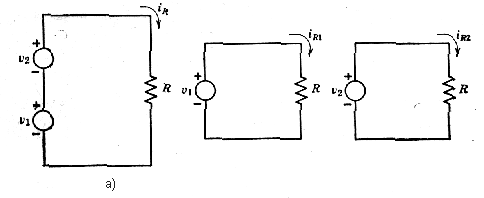
Ilustrácia principu superpozície v lineárnom obvode s 2 nezávislými
zdrojmi
napätia:
|
V obvode na obr. 1h určite prúd I2. Klasickým spôsobom (s použitím Kirchhoffovho zákona pre prúd a napätie a tiež Ohmovho zákona) sa možno presvedčiť, že prúd I1=U0/(R1+R2)-I0R1/(R1+R2) a hľadaný prúd I2=U0/(R1+R2)+ I0R1/(R1+R2) - prúdy sú teda súčtom dvoch členov, z ktorých každý je úmerný pôsobeniu jedného nezávislého zdroja. Alebo inými slovami sa potvrdzuje, že v lineárnom obvode je prúd vo vetve superpozíciou príspevkov od každého zo zdrojov.
Deaktivácia nezávislých zdrojov prúdu a napätia:
Obrázok 1ia obrázok 1ib ilustruje úpravu
obvodu
po odstránení (nezávislých
zdrojov)
zdroja napätia (náhrada zdroja skratom) a zdroja prúdu (náhrada zdroja
rozpojením obvodu). Po potlačení vplyvu jedného z nezávislých
zdrojov
možno získať v zjednodušenom obvode príslušné riešenia (IR2A a
IR2B) a pomocou nich hľadaný výsledok I2=IR2A+IR2B=U0/(R1+R2)+I0R1/(R1+R2).
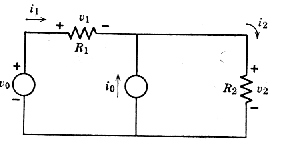 |
Obr. 1h. Ilustrácia principu superpozície v lineárnom obvode s nezávislým zdojom napätia U0 a prúdu I0:
|
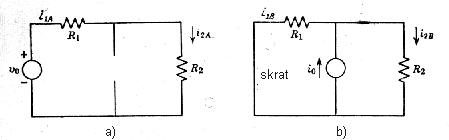 |
Obr. 1i. Náhradný
obvod:
|
Príklad 1b - ilustrácia použitia grafického riešenia obvodu s nelineárnou súčiastkou
Grafická metóda analýzy elektrických
obvodov sa
používa hlave pri výklade pre svoju názornosť. Za predpokladu ak
poznáme
napätie zdroja U0 a odpor R (t.j. ak poznáme zaťažovaciu
charakteristiku
zdroja s napätím naprázdno U0 a vnútorným odporom R) možno
pre
dve neznáme veličiny obvodový prúd I a napätie U zostaviť dve nezávislé
rovnice:
| RI + U - U0 =0 | - symbolický zápis pre priamku s priesečníkom I=U0/R na osi y a U=U0 na osi x . |
| U=f(I) | - symbolický zápis pre nelineárnu V-A charakteristiku súčiastky. |
Riešením sústavy (obr. 1j.) je dvojica
hodnôt
UP a IP (súradnice pracovného bodu P -
priesečníku
oboch čiar).
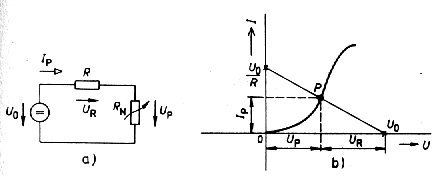 |
Obr. 1j. Grafické
riešenie stanovenia
pracovného bodu v obvode s nelineárnou súčiastkou a zdrojom
napätia:
|
| q | Théveninov a Nortonov náhradný obvod |
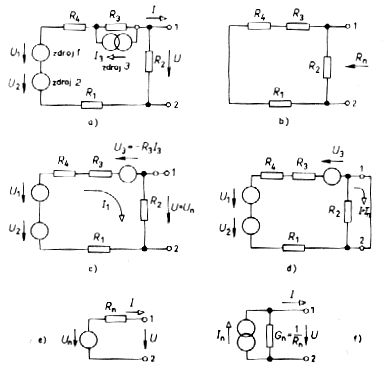
Obrázok 2a ilustruje spôsob, ktorým možno ľubovoľný zložitý lineárny obvod so zdrojmi napätí a prúdov nahradiť vzhľadom na zvolenú dvojicu svoriek jedným náhradným zdrojom a jedným náhradným odporom. Podľa Théveninovej poučky (F)možno túto náhradu (obrázok 2ba) vykonať pomocou náhradného zdroja napätia UTha sériove zapojeného náhradného odporu RTh. (Obecne platí Théveninova poučka nielen pre jednosmerné zdroje a odpory, ale aj pre impedancie a napr. aj pre operátorové vyjadrenie napätí a prúdov.)
Napätie náhradného zdroja UTh
sa rovná
napätiu naprázdno medzi uvažovanými svorkami. Odpor (impedancia)
náhradného
rezistora RTh sa rovná odporu medzi týmito svorkami, ak sú
vyradené
všetky zdroje (ideálne zdroje napätia v pôvodnom obvode nahradíme
skratmi
a ideálne zdroje prúdu nahradíme prerušením obvodu).
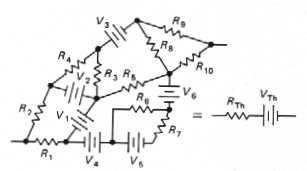 |
Obr. 2a. Princíp náhrady zložitého jednobranu zloženého z rezistorov a zdrojov napätia jediným náhradným obvodom RTh a zdrojom napätia UTh. |
Podľa Nortonovej poučky (obrázok
2bb F)
možno ten istý obvod nahradiť paralelným spojením ideálneho náhradného
zdroja prúdu ITh a toho istého náhradného rezistora RTh.
Prúd náhradného zdroja ITh sa rovná prúdu nakrátko medzi
uvažovanými
svorkami.
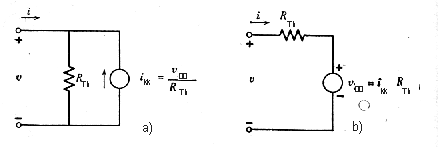 |
Obr. 2b.
Tvar náhradného obvodu podľa:
|
Príklad 2a - ilustrácia použitia princípu Théveninovej poučky na riešenie obvodu
Vytvorme Théveninov náhradný obvod zapojenia na obr. 2ca (t.j. aj obvodu na obr. 1h z príkladu 1). Na obr.2cb je obvod, v ktorom sú nezávislé zdroje nahradené nulovými zdrojmi napätia U0=0 a prúdu I0=0, na základe ktorého možno určiť náhradný odpor RTh=R1||R2=R1R2/(R1+R2).
Ďalším krokom je stanovenie napätia
naprázdno
na svorkách A-Á, ktoré možno určiť pomocou superpozície, podobne ako v
predošlom prípade UTh=R2U0/(R1+R2)+I0R1R2/(R1+R2).
Výsledný náhradný obvod je na obrázku 2cc.
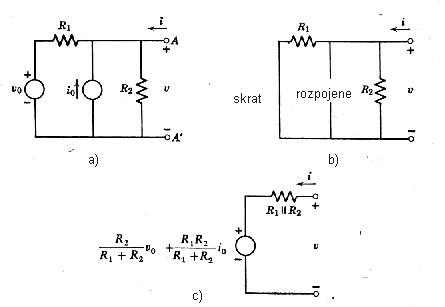 |
Obr.
2c. Náhradný obvod
zapojenia z obrázku 1h:
|
Príklad 2b -
porovnanie
riešenia obvodu pomocou Théveninovej a Nortonovej poučky
 |
Obr. 2d
Princíp náhrady zložitého jednobranu:
|
| q | Ovládané (závislé, neautonómne) zdroje |
Ak obsahuje dvojbran nezávislý zdroj,
môže trvale
dodávať činný výkon a nazýva sa tiež autonómnym zdrojom. Ak
obsahuje
dvojbran pasívne prvky a ovládané zdroje (závislé na niektorom
napätí
alebo prúde v iných častiach obvodu), môže sa za istých podmienok
chovať
ako zdroj, avšak samostatne nemôže dodávať činný výkon. Takýto dvojbran
sa považuje za aktívny a nazýva sa neautonómnym(závislým,
ovládaným). Do
tejto kategórie patria napríklad dvojbrany obsahujúce tranzistory,
operačné
zosilňovače a pod. Pri tvorbe náhradného obvodu pomocou principu
superpozície
sa neautonómne zdroje neodstraňujú!
Príklad 3 a príklad 4 ilustrujú
najjednoduchčie tvary typických dvojbranov - s veľmi vysokým / veľmi
nízkym vstupným odporom na vstupnom porte resp. napäťovým / prúdovým
zdrojom na výstupe. Príklad 4 a 5 ilustrujú obtiaže, ktoré vznikajú,
keď nie je možné jednoducho rozddeliť dvojbran na nezávislé, od seba
oddelené časti - vstupnú a výstupnú.
Príklad 3 - ilustrácia použitia neautonómneho zdroja napätia ovládaného napätím
Obrázok. 2e ilustruje príklad
neautonómneho zdroja
napätia uout ovládaného napätím u1, ktoré vzniká
v inej vetvi obvodu, v dôsledku pôsobenia generátora s napätím ug.
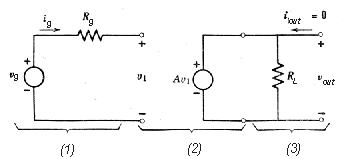 1- vstupný generátor 2 - ovládaný (neautonómny) zdroj 3 - záťaž (výstup) |
Obr. 2e. Príklad neautonómneho zdroja napätia uout ovládaného napätím u1. Nakoľko vo vetvi s generátorom netečie prúd ig je napätie u1=ug- igRg=ug takže výstupné napätie uout=Aug je úmerné vstupnému napätiu ug. Ak je A>1 tak je uout>u1 a ovládaný zdroj sa správa ako lineárny zosilňovač so zosilnením A. |
Príklad 4 - ilistrácia použitia neautonómneho zdroja prúdu ovládaného prúdom
Na obrázok. 2f je príklad neautonómneho
zdroja
prúdu iC=bFiB,
ovládaného prúdom iB, ktorý vzniká v inej vetvi obvodu, v
dôsledku
pôsobenia generátora s napätím ug. Nakoľko vo vetvi s
generátorom
tečie prúd iB=ug/Rg a na výstupe sa
predpokladá,
že iout=0 (prúd cez zaťažovací odpor RL je bFiB)
je na výstupe napätie uout=Ucc-bFRLug/Rg.
(Takáto závislosť uout=f(ug), odmeraná pri
stálom tvare napätia sa nazýva prevodová charakteristika. Na
rozdiel
od závislosti výstupného napätia od frekvencie F(w)=uout(w),
ktorá sa volá - prenosová charakteristika.)
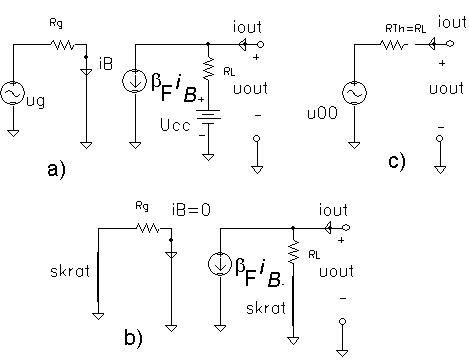 |
Obr. 2f. Príklad
neautonómneho
zdroja prúdu iC=bFiB,
ovládaného prúdom iB a jeho Théveninov náhradný obvod.
|
Príklad 5 - použitie pomocného zdroja prúdu in na určenie vnútorného odporu RTh náhradného obvodu s neautonómnym zdrojom prúdu
Ak výstup neautonómneho zdroja nejakým
spôsobom
naviazaný na vstup, t.j. ak existuje v obvode spätná väzba nemusia v
obvode
existovať nezávislé zdroje a teda v obvode nemôže vzniknúť napätie
naprázdno
a prúd nakrátko. Na obrázku 2ga je obvod s neautonómnym zdrojom prúdu bFiB,
ovládaného prúdom iB, bez prítomnosti nezávislých zdrojov
prúdu
alebo napätia. Prúd iin=iB bude pretekať len v
prípade
existencie nejakého vstupného napätia uin. Ak sa teda podarí
pomocou vonkajšieho pomocného zdroja prúdu in=iB
vytvoriť rovnaké prúdy a úbytky napätí na odporoch ako v pôvodnom
zapojení
možno z obvodu určiť Théveninov odpor RTh jeho náhradného
obvodu.
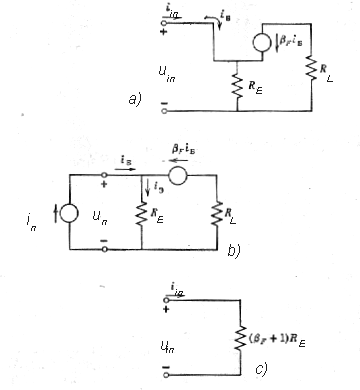 |
Obr. 2g.
Zapojenie s neautonómnym zdrojom prúdu iC=bFiB
bez prítomnosti nezávislych zdrojov prúdu alebo napätia.
|
Príklad 6 - použitie pomocného zdroja napätia un na určenie vnútorného odporu RTh náhradného obvodu s neautonómnym zdrojom prúdu ovládaného prúdom
Na obrázku 2ha je obvod s
neautonómnym zdrojom
prúdu bFiB,
bez prítomnosti nezávislych zdrojov prúdu alebo napätia. Podobne ako v
príklade 5, ak sa podarí pomocou vonkajšieho pomocného zdroja napätia un
vytvoriť rovnaké prúdy a úbytky napätí na odporoch ako v pôvodnom
zapojení,
možno z obvodu určiť Théveninov odpor RTh jeho
náhradného
obvodu.
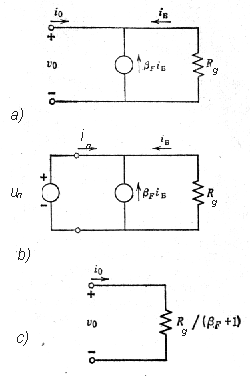 |
Obr. 2h
Zapojenie s neautonómnym zdrojom prúdu iC=bFiB bez
prítomnosti nezávislých zdrojov prúdu alebo napätia.
|
| q | Signály |
Pravidlá pre analýzu jednosmerných obvodov (Ohmov zákon, Théveninova poučka a pod.) sú použiteľné aj pre obvody s meniacou sa v čase amplitúdou prúdu alebo napätia. Vhodne upravené napätie alebo prúd môžu byť ako signál použité na prenos správ alebo údajov. Informácia môže byť pri harmonickom tvare nosiča informácie zakódovaná pomocou namodulovanej amplitúdy, frekvencie, fázy alebo aj iným spôsobom, napr. pomocou postupnosti impulzov.
Na základe impulzu z niektorých detektorov ionizujúceho žiarenia možno získať informáciu o pohltenej energii častice v objeme detektora, o mieste a čase prieletu častice, poprípade aj identifikovať typ častice. Takéto detektory ionizujúceho žiarenia sú teda zdrojmi impulzného signálu (v tvare napätia, prúdu alebo náboja).
Nasledujúce obrázky ilustrujú niektoré
často používané
tvary signálov.
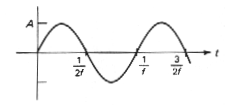 |
Obr.
3a. Tvar harmonického napäťového signálu u(t)=Asin(2pft+j) s frekvenciou f, periódou T=1/f fázou j a amplitúdou A. |
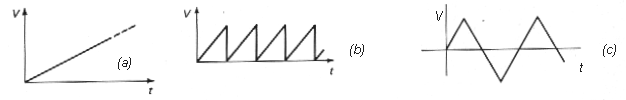 |
Obr. 3b. Tvar
pílovitého signálu:
|
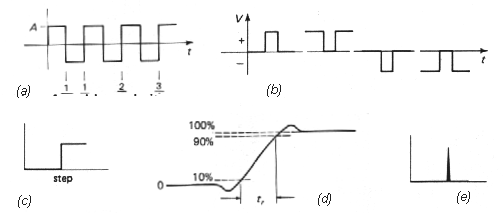 |
Obr. 3c. Impulzný
signál:
|
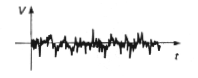 |
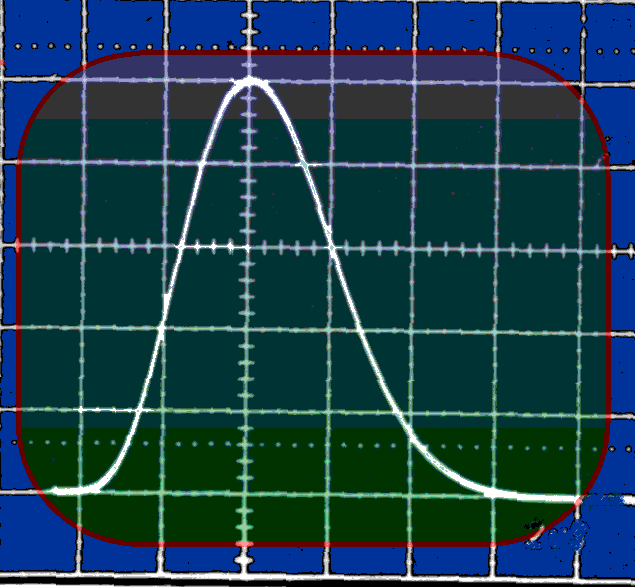
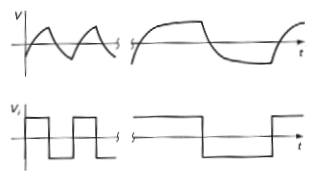
Obr. 3d. Ilustrácia osciloskopického priebehu šumového napätia, ktoré na rozdiel od signálu má náhodnú povahu. Šum býva charakterizovaný spektrálnou hustotou a frekenčným spektrom (šírkou frekvenčného pásma). |
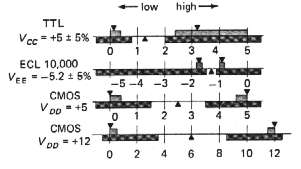 |
Obr. 3e. Napäťové úrovne zodpovedajúce vysokej HIGH a nízkej LOW úrovni pre rôzne typy logických obvodov (Šipka označuje rozhodujúcu úroveň Ur pri ktorej sa mení úroveň, napr. pre TTL je Ur=1,4V). |
| q | Charakterizovanie prenosových vlastností pasívnych dvojbranov |
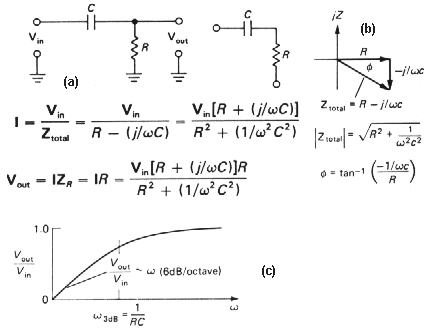
Dvojbrany sú spravidla súčasťou prenosovej cesty medzi zdrojom a spotrebičom. V elektronike sú typickými dvojbranami deliče napätia a prúdu, zosilňovače, oneskorovacie vedenia, frekvenčné filtre, prispôsobovacie články, derivačné a integračné obvody. Frekvenčné vlastnosti týchto dvojbranov dobre vyjadrujú ich obvodové funkcie. Delia sa na prenosové funkcie, ktoré vyjadrujú informáciu o prenose signálu z jednej brány na druhú (napríklad prenos napätia Ku=Uout/Uin) a imitačné funkcie, ktoré vyjadrujú vzťahy medzi napätím a prúdom dvojbranu (napríklad komplexná vstupná impedancia Zin = Uin / Iin).
V lineárnych obvodoch so zdrojom harmonického signálu, ktorý má frekvenciu w =2pf sú obvodové funkcie komplexnými funkciami frekvencie. Napríklad závislosť medzi prúdom a napätím, charakterizovanú komplexnou veličinou Z = Z(w )ejj(w) sa nazýva komplexná frekvenčná charakteristika. Modul kompelxnej frekvenčnej charakteristiky |Z| = Z(w) sa nazýva amplitúdová frekvenčná charakteristika (F)a závislosť argumentu j(w) fázová frekvenčná charakteristika (F).
Vhodným grafickým vyjadrením frekvenčných charakteristík (Bodeho metóda F) možno dosiahnuť, že sú do značnej miery nezávislé na parametroch sledovaného obvodu (použitie označenia t pre časovú končtantu namiesto RC, L/R a pod.), že platia pre veľký frekvenčný rozsah (logaritmická mierka, normovanie - vynášanie pomerných hodnôt: w /w0 na pozdĺžnu os a A/A0 na zvislú os) a že amplitúdové charakteristiky možno aproximovať asymptotami k skutočnému priebehu.
Vo väčšine elektronických obvodov sa
požadujú
vlastnosti blízke lineárnym obvodom. Napríklad v zosilňovači požadujeme
neskreslený prenos, t.j. aby okamžité hodnoty výstupného napätia
(prúdu)
boli k-násobkom zodpovedajúcich hodnôt napätia (prúdu) na vstupe, kde k
je zosilnenie. To bude splnené, ak bude zosilnená každá harmonická
zložka
vstupného signálu rovnako a ak budú zachované fázové posuny medzi
týmito
zložkami tak ako v lineárnom obvode (t.j. bez amplitúdového a fázového
skreslenia). V ideálnom zosilňovači by teda amplitúda signálu na
výstupe
mala závisieť len od vstupnej amplitúdy a nemala by závisieť od
frekvencie
signálu. V reálnom zosilňovači (F)
sú tieto podmienky splnené len približne a to ešte len v istom
frekvenčnom
intervale; hovoríme o frekvenčnom pásme, v ktorom sú podmienky
splnené
s danou odchýlkou (napríklad odchýlkou d<=10%).
Okrem toho reálny zosilňovač je schopný zabezpečiť lineárny prenos
signálu
len do určitého (tzv. dynamického) rozsahu amplitúdy, pokiaľ sa nezačne
prejavovať nelinearta charakteristík elektronických prvkov - diód,
tranzistorov
a pod.
Impulzný signál
možno interpretovať
- ako neharmonický podnet, a ten analyzovať ako superpozíciu priebehov (analýza metódou Fourierovho radu - obr. 3f.), pozozstávajúcich z :
- jednosmernej zložky a
- harmonických priebehov s frekvenciami w0, 2w0, 3w0, atď (teda s frekvenciami kw0), ktoré sú násobkami základnej frekvencie w0 (harmonických zložiek) s vhodnými amplitúdami, podobne ako pri aproximácii funkcie pomocou Fourierovho radu.
- ako superpozíciu vstupných podnetov definovaného tvaru ak je známa reakcia výstupu obvodu na vstupný podnet definovaného tvaru. Na posúdenie prechodového javu možno použiť :
- skokový impulz -> Vzniknutá odozva na vstupný signál jednotkového skoku 1(t) (obr. 3g) sa nazýva prechodová charakteristika.
- veľmi krátkeho impulzu ->Odozva na vstupný signál tvaru delta funkcie dn(t) (obr. 3h) s infinitívne krátkym trvaním sa nazýva impulzová charakteristika.
Výsledná odozva na výstupe obvodu potom
pozostáva
zo superpozície odoziev jednotlivých frekvenčných zložiek.
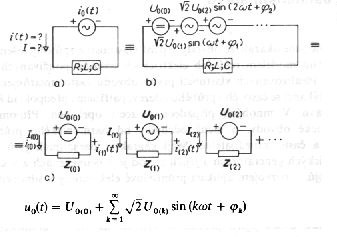 |
Obr. 3f. Objasnenie metódy na príklade zdroja u0(t) pripojeného k jednobranu, zloženého z R,L,C. Analýza obvodu je založená na superpozícii postupného pôsobenia jednotlivých zdrojov napätia (jednosmerného zdroja U0(0), zdroja U0(1) s frekvenciou w až zdroja U0(k) s frekvencii kw). |
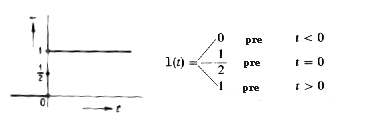 |
Obr. 3g Jednotková funkcia 1(t), ktorá zjednodušuje popis nulových počiatočných podmienok prechodového javu. |
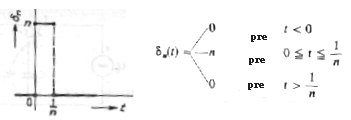 |
Obr. 3h. Diracova "funkcia" dn(t), na uľahčenie definovania okamžitých amplitúd impulzov prechodového javu. |
Výsledná odozva (F
Laplacceova transformácia) na výstupe obvodu potom
pozostáva zo
superpozície
odoziev jednotlivých charakteristík (prechodových alebo impulzných
metódou
Duhamelovho integrálu - obr. 3i).
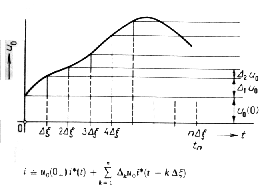 |
Obr. 3i. Vstupný impulzný priebeh u0(t) môže byť predstavený ako postupnosť oddelených napäťových impulzov (na obrázku v tvare jednotkových skokov 1(t)). Ak je známa reakcia obvodu na jednotkové skoky - prechodová charakteristika obvodu, tak výslednú reakciu obvodu možno určiť pomocou Duhamelovho integrálu ako superpozíciu prechodových charakteristík (na obrázku posunutých o interval Dx) |
F Prechodné
javy v RC a RL obvodoch
| q | RC články s hľadiska prechodového javu |
RC články (jednobrany alebo tiež aj dvojpóly) sa používajú veľmi často v obvodovej technike. Pri analýze prúdu a napätia sa používajú dva prístupy:
- Spôsob založený na sledovaní časových zmien (prechodových javov) u(t) a i(t);
- Spôsob založený na sledovaní frekvenčnej závislosti amplitúdy A(w) a fázy j(w) napätia alebo prúdu.
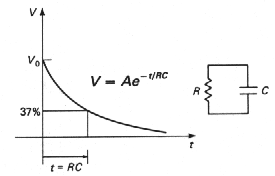 |
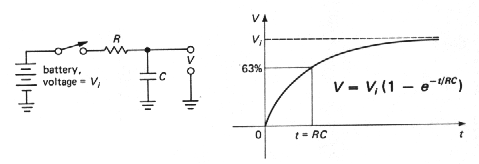
Obr. 4a. Prechodový jav u(t)= U0exp(-t/RC) vybíjania kondenzátora C, nabitého na napätie U0 cez paralelne pripojený odpor R (-rýchlosť vybíjania charakterizuje časová konštanta t=RC). |
 |
| Obr. 4b.
Vybitý kondenzátor (UC=0) sa po zapnutí spínača bude nabíjať u(t)=U0[1-exp(-t/RC)] s rýchlosťou, ktorú určuje časová konštanta t=RC. Za trvanie t>>RC (za t=5RC sa ustáli napätie s presnosťou 1%) na svojej konečnej hodnote. |
 |
Obr. 4c Tvarovanie impulzov obdĺžnikovitého tvaru pomocou RC článku. Trvanie čela impulzu merané od úrovne 10% po úroveň 90% tzv. aktívne trvanie čela impulzu tca=2,2RC. |
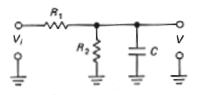 |
Obr. 4d. Ilustrácia použitia Théveninovej poučky. Výsledný odpor R=R1||R2 náhradného obvodu (obr. 4e) a časová konštanta t=(R1||R2)C. |
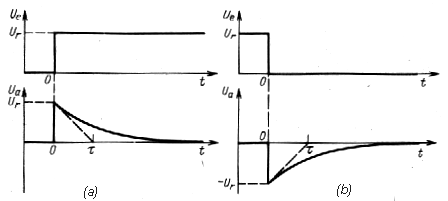
Integračný článok RC
 |
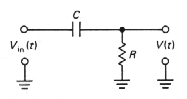
Obr. 4e. Integračný RC článok. |
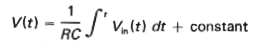 |
 |
| Obr. 4g.
Reakcia RC integračného článku na skokovú zmenu napätia:
(t=RC - časová konštanta) |
 |
Obr. 4h. Tvarovanie pílovitých impulzov z impulzov obdĺžnikovitého tvaru pomocou integračného RC článku. Prvá časť exponencialy je ako integrál z konštanty lineárne narastajúca. Čím menšiu časť exponencialy využijeme tým je priamková aproximácia presnejšia. |
 |
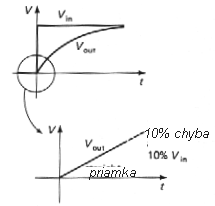
Obr. 4i. Integračný článok RC (R=15kW, C-1000pF) ako oneskorovací obvod. Trojuholníkové symboly na obrázku reprezentujú logické obvody CMOS, ktorých úlohou je oddeliť obvody a tiež tvarovať impulzy (po uplynutí ~0,7RC=10ms dosiahne prechodový jav napätia B na kondenzátore 50% výstupnej amplitúdy, čo je rozhodujúca úroveň pri ktorej sa zmení stav výstupu C obvodu CMOS) |
FKontróla tvarovania impulzov pomocou integračného článku v praktikovej úlohe 2
Derivačný článok CR
 |
Obr. 5a. Obvodová realizácia derivačného CR článku. |
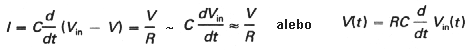 |
- u(t)=Ur.1(t);
- u(t)= - Ur.1(t).
 |
| Obr. 5b.
Reakcia CR derivačného článku na skokovú zmenu napätia: |
(t=RC - časová konštanta)
- Obvodová realizácia.
- Tvarovanie obdĺžnikovitých impulzov pomocou derivačného CR článku (generujú sa ihličkovité impulzy krátkeho trvania - obr. 3ce).
- Možný dôsledok kapacitnej väzby na tvar signálu.
 |
| Obr. 5c.
Derivačný CR článok: |
Tvarovanie impulzov korelovaných s čelom a tylom vstupného obdĺžnikového impulzu a následný výber kladného impulzu (a jeho tvarovanie na obdĺžnikovitý tvar).
FKontróla tvarovania impulzov pomocou derivačného článku v praktikovej úlohe 3
RL články
Použitie pojmu časová konštanta (t=RC a t=R/L) umožňuje zapísať prechodové javy v RC a RL obvode obdobnými vzťahmi. Napätie na indukčnosti uL(t)=U0exp(-t/t) a RL článok má vlastnosti derivačného obvodu. Napätie na odpore uR(t)=U0[1-exp(-t/t)] a LR článok má vlastnosti integračného obvodu.FKontróla tvarovania impulzov pomocou impulzného transformátora v praktikovej úlohe 4
F R,
L, C v obvode striedavého prúdu
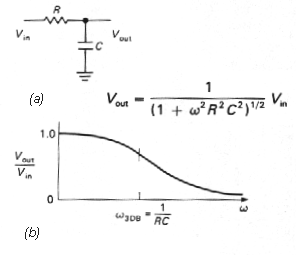
| q | RC články ako frekvenčné filtre |
Kombinácia odporu R a kondenzátora C
môže byť
tiež chápaná pre harmonické signály ako frekvenčne závislý delič,
ktorého
vlastnosti závisia od umiestenia impedancie Z=-j/wC
v deliči.
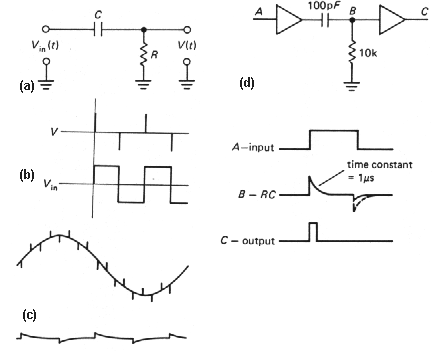
Dolnopriepustný filter (F)
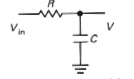
Napäťový RC delič zapojený podľa obrázku 6a má vlastnosti dolnopriepustného filtra nakoľko pre nízke frekvencie (až po hornú hraničnú frekvenciu fh<=1/2pRC) je amplitúda na jeho výstupe Uout približne rovnaká ako na vstupe Uin.
 |
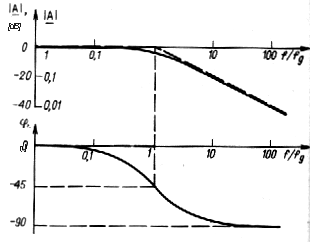
Obr.
6a. Dolnopriepustný RC filter a jeho amplitúdová frekvenčná charakteristika (horná hraničná frekvencia fh=1/2pRC pri ktorej je pomer amplitúd Uout/Uin=1/(2)0.5 ~ - 3dB). |
- |A|=1, čomu zodpovedá 0dB (decibel dB=20log10(Uout/Uin) umožňuje jednoducho porovnať amplitúdy dvoch signálov) v oblasti frekvencii f<<fg, (frekvencia zodpovedajúca zlomu fg=fh je v danom prípade horná hraničná frekvencia fh).
- v oblasti vysokých frekvencii f>>fg, je |A|~1/(wRC) t.j. pomer amplitúd |A|=Uout/Uin je nepriamo úmerný frekvencii. Pri 10 násobnom zvýšení frekvencie sa |A| zmenší 10 krát, teda o 20 dB.
- pri frekvencii f=fh=fg je |A|=Uout/Uin=1/(2)0.5 , teda pokles o - 3dB (resp. odchylka aproximácie od skutočného priebehu frekvenčnej charakteristiky).
- Amplitúdová frekvenčná charakteristika dolnopriepustného RC filtra
- Fázová frekvenčná charakteristika dolnopriepustného RC filtra ( pri hornej hraničnej frekvencii fh=1/2pRC je fázový posun j=45°)
 |
Obr. 6b. Bodeho tvar frekvenčných charakteristík (Amplitúda je zobrazená v logaritmických jednotkách decibeloch - dB a na osi frekvencii je použitá relatívna logaritmická mierka) |
Hornopriepustný filter (F)
Napäťový CR delič zpojený podľa obrázku 6c má vlastnosti hornopriepustného filtra nakoľko pre vysoké frekvencie (f >=1/2pRC) je amplitúda na jeho výstupe Uout približne rovnaká ako na vstupe Uin. Napríklad RC člen s R=1kW a C=0,01mFmá dolnú hraničnú frekvenciu (pri ktorej je pokles o 3 dB) fd=15,9kHz.
 |
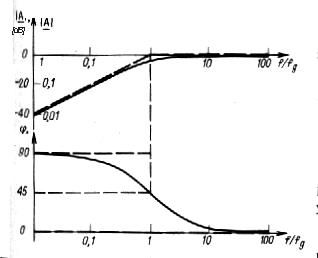
| Obr. 6c. Hornopriepustný CR filter a jeho amplitúdová frekvenčná charakteristika (dolná hraničná frekvencia fd=1/2pRC pri ktorej je pomer amplitúd Uout/Uin=1/(2)0.5 ~ -3dB) |
- |A|=1, čomu zodpovedá 0dB (decibel dB=20log10(Uout/Uin) umožňuje jednoducho porovnať amplitúdy dvoch signálov) v oblasti vysokých frekvencii f>>fg, (frekvencia zodpovedajúca zlomu fg=fd je v danom prípade dolná hraničná frekvencia fd).
- v oblasti nízkych frekvencii f<<fg, je |A|~wRC t.j. pomer amplitúd |A|=Uout/Uin je priamo úmerný frekvencii. Pri 10 násobnom zvýšení frekvencie sa |A| zvýši 10 krát, teda o 20 dB.
pri frekvencii f=fd=fg je |A|=Uout/Uin=1/(2)0.5 , teda pokles o - 3dB (resp. odchylka aproximácie od skutočného priebehu frekvenčnej charakteristiky).
- Amplitúdová frekvenčná charakteristika hornopriepustného CR filtra
- Fázová frekvenčná charakteristika hornopriepustného CR filtra ( pri dolnej hraničnej frekvencii fd=1/2pRC je fázový posun j=45°)
 |
Obr. 6d. Bodeho tvar frekvenčných charakteristík (Amplitúda je zobrazená v logaritmických jednotkách decibeloch - dB a na osi frekvencii je použitá relatívna logaritmická mierka) |
FKontrola parazitnej kapacity odporového deliča v praktikovej úlohe 1
| q | Parametre umožňujúce porovnať frekvenčnú a prechodovú charakteristiku |
S použitím vzťahov pre časovú konštantu t=RC integračného a derivačného článku a hraničné frekvencie wh=2pfh=1/RC dolnopriepustného a wd=2pfd=1/RC hornopriepustného RC filtra možno získať vzťah:
- medzi hornou hraničnou frekvenciou dolnopriepustného filtra fh a skreslením trvania čela výstupného impulzu tca=2,2t.. Obvod RC tým menej predlžuje (aktívne) trvanie čela impulzu tca, čím má obvod vyššiu hornú hraničnú frekvenciu :
| fh~2,2 /(2ptca)~ (0,35)/tca |
- medzi dolnou hraničnou frekvenciou obvodu fd a skreslením tvaru impulzu o trvaní ti (Prípustná deformáciou tvaru impulzu vyjadrená ako 10% relatívny pokles amplitúdy impulzu d=DU/U na konci trvania impulzu ti). Čím je teda dolná hraničná frekvencia obvodu fd nižšia, tým je relatívny pokles amplitúdy impulzu d=DU/U na konci trvania impulzu ti menší:
| fd~d/(2p t i)~0,16d/t i |
Zosilňovače, ako aj ďalšie iné prenosové
zariadenia
majú v dôsledku existencie vlastných integračných a derivačných článkov
v zariadení obmedzený frekvenčný prenos aj v oblasti nízkych tak aj v
oblasti
vysokých frekvencii. Hovori sa, že existuje určité frekvenčné pásmo
obvodu Df=fh-fd
, v ktorom má obvod neskreslený prenos so stálym súčinitľom prenosu.