Laplacceova transformácia

Pri analyze obvodov s ustálenými priebehmi harmonických prúdov a napätí používa symbolicko komplexná metóda, ktorá - namiesto pôvodného priebehu harmonickej časovej závislosti, napr. u(t)=Umcos(w t+j) požíva reálnu zložku funkcie formálne namiesto derivácie vyskytuje násobenie -jw a namiesto integrálu delenie -jw . Napr. komplexná impedancia zložená z R, L, a C má v tejto reprezentácii tvar:
 Z=R+ jw L+1/( jwC).

Pri riešení prechodových javov v obvodoch, po sformulovaní rovníc pre prúdy  a napätia, možno okrem klasickej metódy riešenia lineárnych integrálno-diferenciálnych rovníc s konštantnými koeficientmi použiť operátorovú metódu obrazových rovníc, ktorá je založená na vytvorení Laplacceovho obrazu z časových závislostí prúdov a napätí v obvode, a tým na pretransformovaní integrálno-diferenciálnych rovníc na algebraické. Po nájdení riešenia algebraických obrazových rovníc potom treba ešte vykonať spätnú Laplacceovu transformáciu obrazu odozvy na orginál odozvy.

Princíp ilustruje obrázok. La1
 
Obr. La1. Postup pri riešení prechodových javov v obvode.

Operátorový tvar funkcie F(p) - obraz orginálu f(t)


 

 
 
Napríklad obrazom funkcie e-pt je 1/(p-a), nakoľko:

 
 
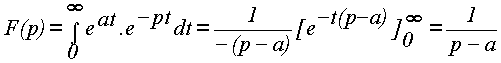"Slovník"  Laplaceovej transformácie
 pre niektoré často používané funkcie.
Tab. Laplacceova transformácia pre niektoré často používané funkcie

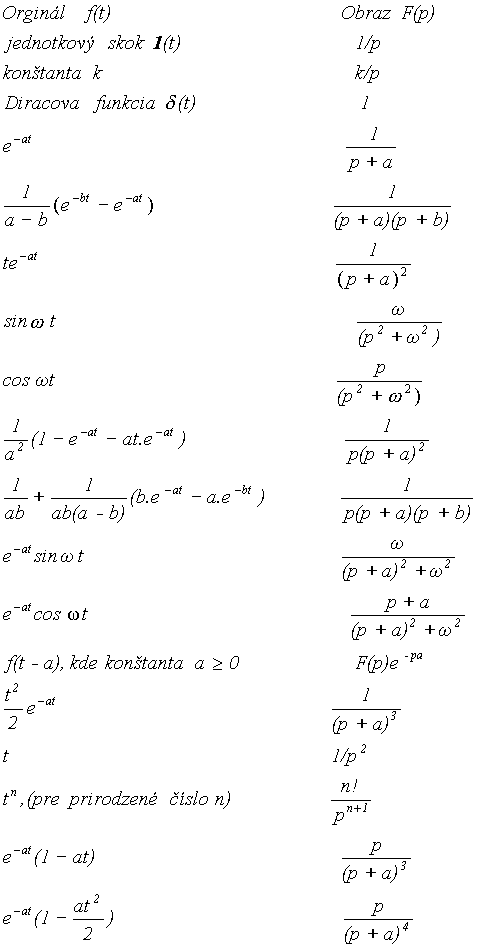 Význam Laplacceovej transformácie

Laplacceova transformácia má pre teóriu obvodov hlbší význam, než len ako obyčajná matematická metóda. V obore komplexnej premennej p – v obrazovom obore, platí medzi obrazom napätia a prúdu operátorové vyjadrenie Ohmovho zákona. Platia tiež Kirchhoffove zákony v operátorovom tvare. Tiež možno použiť známe metódy analýzy obvodov, napr. Theveninovu vetu a pod. Napr. obrazová impedancia - operátorový tvar impedancie Z, zloženej z R, L a C je:

Z(p)=R+ pL+1/(pC).

Operátorová metóda riešenia integrálno-diferenciálnych rovníc s konštantnými koeficientami je pre prax výhodná. Pri jej použití odpadá určovanie integračných konštánt. Operátorová metóda umožňuje nahradiť derivovanie násobením - p a integrovanie delením -p (analogicky ako pri analýze ustáleného stavu obvodov s harmonickým napätím alebo prúdom, v ktorej p=jw ).

Prednosťou klasického spôsobu riešenia diferenciálnej rovnice s konštantnými koeficientmi je však ľahšia fyzikálna interpretácia výsledkov. Obecné riešenie rovnice klasickým spôsobom charakterizuje prechodný jav a partikulárne riešenie charakterizuje ustálený stav.
 

Niektoré odozvy , potrebné pre prax s RLC obvodmi ilustruje obr.La3.
 
Obr. La3. Príklad  aplikovania Laplacceovej transformácie - transformácia derivovania na násobenie - p a integrovania na delenie - p
    iL(0) - prúd cez indukčnosť v čase t=0
    uC(0) - napätie na kondenzátore v čase t=0

Demo príklad - porovnanie klasického riešenia s operatorovým:

 
Obr. La4. 
K sériovému RL článku je v okamihu t=0 pripojený zdroj jednosmerného napätia U0 . Nájdite odozvu prúdu i(t)?

 

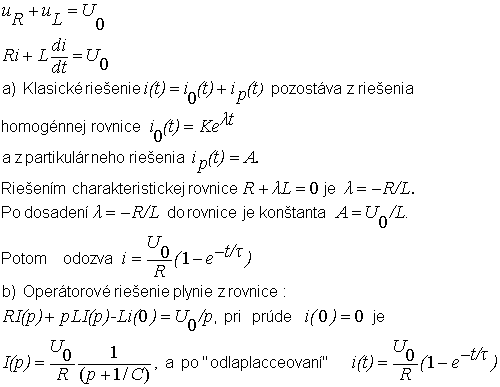Priklad 2:

Obvod na obrázku predstavuje dynamický náhradný obvod unipolárneho tranzistora v oblasti malých signálov (s kapacitami Cm a Cp ) - ako príklad ovládaného zdroja prúdu gmup , riadeného napätím up. V operátorovom tvare na základe Laplacceovej transformácie určite náhradný obvod z hľadiska výstupného odporu RL.
 

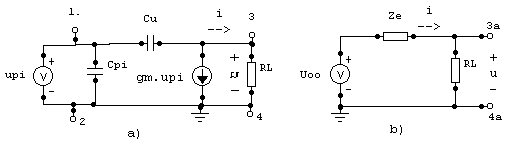Obr. La5 k príkladu 2  (upi=up; Cpi=Cp; Cu=Cm ; gm.upi=gmup)

Podľa Kirchhoffovho zákona pre uzol 3a na obr. La5 platí:

Na základe analógie s Theveninovým ekvivalentným obvodom, u ktorého platí (podobne ako na obr. La5b):

U(p)=-ZeI(p)+Uoo(p),

Predstavujú členy v predchádzajúcom vzťahu :

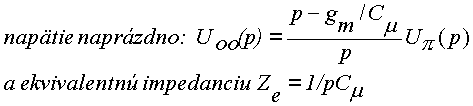
Na základe náhradného obvodu na obr. La5b je operátorový tvar napätia na výstupe


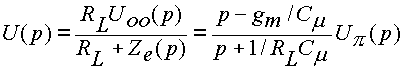
Zber náboja - integrácia prúdového impulzu

Pomocou lineárneho RC článku na obr. La6, za predpokladu, že napätie uC(t)<<u(t), možno  uskutočniť integráciu priebehu napätia u(t). Tento predpoklad možno splniť pri trvaní impulzu ti<<t =RC. Potom je výstupné napätie :
 
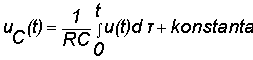   (1)

 
 
Obr. La6. 
Integračný RC článok
 

 

 
 
 
Obr. La7. 
Náhradný obvod detektora ako príklad RC obvodu na integráciu prúdového impulzu z detektora. Odpor R1.predstavuje pracovný odpor detektora, kondenzátor C1 zase kapacitu . detektora

Pre presnejšie integrovanie sa namiesto jednoduchých RC článkov používajú zapojenie integračných zosilňovačov, v jadrovej elektronike tiež známych pod názvom nábojovo citlivé predzosilňovače.

 
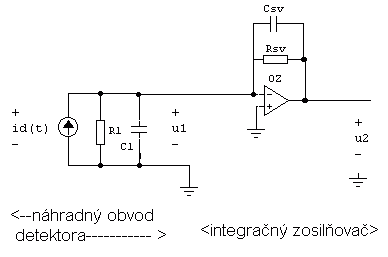Obr. La8 . 
Integračný zosilňovač (odpor Rsv slúži len na nastavenie zosilnenia Au=u2/u1~-Rsv/R1 pomocou jednosmernej spätnej väzby. Pre integrovanie má rozhodujúci vplyv časová konštanta t =R1Csv.

V zosilňovači na obr. La8 je základom spätnoväzobnej impedancie kondenzátor Csv. Ak sa chceme presvedčiť o fungovaní integrácie pomocou takéjto spätnej väzby predpokladajme, že impedancia, ktorú reprezentuje kondenzátor 1/p Csv je podstatne menšia ako odpor Rsv  (=> (1/p Csv ) ||Rsv ~1/p Csv ) a že na kondenzátore sa nachádzal zvyškový náboj Q0, potom v čase t=0 na začatku merania bude výstupné napätie:
 

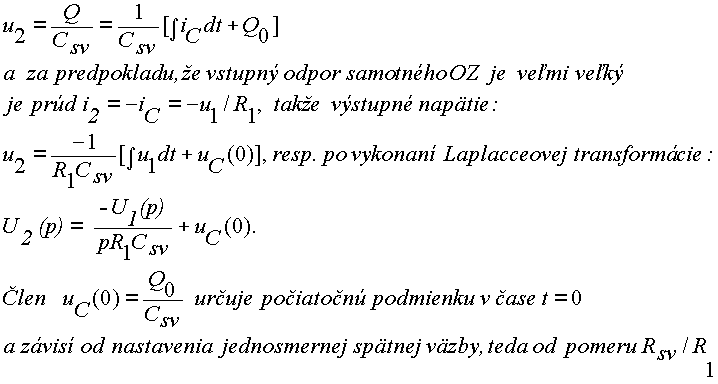Príklad 3 - krátky prúdový impulz d(t)
Určite priebeh napätia UC(t) na kondenzátore v obr. La7 ako reakciu na veľmi krátky prúdový impulz d(t), za predpokladu, že pred pôsobením impulzu bol kondenzátor vybitý a jeho napätie UC(t)=0.
Podľa 1. Kirchhoffovho zákona:
 
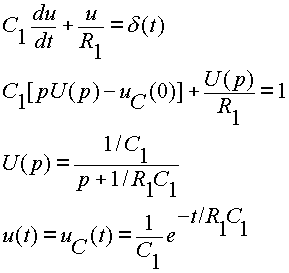Impulz v tvare funkcie d(t) nemožno technicky realizovať.Možno použiť predstavu, že kondenzátor bol nabitý jednotkovým nábojom
v čase t=0 tak, že na ňom sa okamžite ustálilo napätie U=Q/C=1/C. Napätie na kondenzátore sa môže takto okamžite zmeniť len vtedy, ak by bol nabíjací prúd nekonečne veľký.

Príklad 4- prúdový skok Id1(t)
Určite priebeh napätia na výstupe obvodu z obr. La7 ako reakciu na prúdový impulz v tvare skoku Id1(t), za predpokladu, že pred pôsobením impulzu bol kondenzátor vybitý a jeho napätie UC(t)=0.

Podobne ako v predošlom príklade podľa 1. Kirchhoffovho zákona:
 

Príklad 4a - prúdový obdĺžnikovitý impulz
Určite priebeh napätia na výstupe obvodu z obr. La7 ako reakciu na prúdový impulz obdĺžnikového tvaru o trvaní ti a s amplitúdou Id, za predpokladu, že pred pôsobením impulzu bol kondenzátor vybitý a jeho napätie UC(t)=0. Prúdový impulz obdĺžnikového tvaru o trvaní ti s amplitúdou Id realizujte pomocou 2 jednotkových skokov, s opačnou amplitúdou, vzájomne posunutých o trvanie ti. =>  Id [1(t) - 1(t- ti).
Podobne ako v predošlom príklade podľa 1. Kirchhoffovho zákona:
 
 

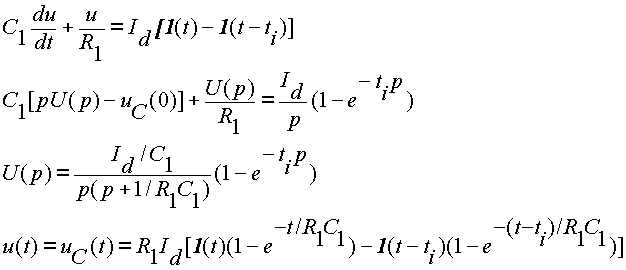Prvá časť riešenia popisuje tvar impulzu v intervale 0<=t<= ti., druhá časť vystihuje riešenie pre t> ti.

Príklad 4b -Vplyv pracovného odporu na vlastnosti detektora

Pre spektrometrické merania s detektorom kvôli dosiahnutiu dokonalej integrácie prúdového impulzu ( F vzťah 1) požadujeme zachovať malý pomer trvania impulzu ti<<t =R1C1 k časovej konštante vstupného obvodu detektora t=R1C1. Trvanie prúdového impulzu z detektora ti závisí od typu detektora a od podmienok realizácie experimentu, napr. pre ionizačnú komoru s mriežkou závisí od doby zberu náboja elektrónovej zložky prúdu ti °~1us. Pri konštrukcii detektora je snahou dosiahnuť minimálnu kapacitu detektora C1, aby sa amplitúda impulzu mohla priblížiť maximálne možnej amplitúde napätového impulzu U10°~ Q/C1 (Takúto amplitúdu napätového impulzu U10°~ Q/C1 možno dosiahnuť len v  idealizovaných podmienkach registrácie ojedinelej udalosti, pomocou nekonečného odporu R1 - teda pri časovej konštante t =inf.) Prakticky teda možno optimalizovať pomeru ti/t len zmenou pracovného odporu R1 detektora. Pre názornejšie predstavu o voľbe pomeru ti/t sme použili na vyjadrenie náboja Q= U10.C1=Id.ti maximálne možnú amplitúdu napätového impulzu U10°~ Q/C1 a z tohto vyjadrenia vyplývajúcu amplitúdu prúdového impulzu, Id=U10ti/C1 na dosadenie do výsledného vzťahu z príkladu 4a pre napätie UC(t): 
 
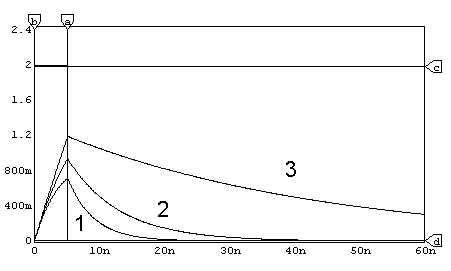Obr. La9 ilustruje priebeh napätia uC(t) pre rôzne časové konštanty t=R1C. (pri trvaní impulzu ti = 30ns a C1=100pF pre R11=40W ; R12=80W ; a R13=400W. Vhodnú veľkosť pracovného odporu R1 volíme ako optimum medzi získaním čo najväčšej amplitúdy na výstupe detektora a operačnou rýchlosťou detektora - podľa požiadaviek experimentu

 
Obr. La9. 
Závislosť amplitúdy napätia na kondenzátore uc(t) v Integračnom RC článku pri rôznom pomere ti/t - pri impulze o trvaní tI=30ns a C1=100pF od R11=40W ; R12=80W ; R13=400W

 

Príklad 5 - napäťový obdĺžnikovitý impulz
Určite priebeh prúdu v obvode a napätia uC(t) na výstupe obvodu z obr. La6 ako reakciu na krátky obdĺžnikovitý napäťový impulz o trvaní ti s amplitúdou Ud, za predpokladu, že pred pôsobením impulzu bol kondenzátor vybitý a jeho napätie UC(t)=0. Napäťový impulz obdĺžnikového tvaru o trvaní ti a s amplitúdou Ud realizujte pomocou 2 jednotkových skokov, s opačnou amplitúdou, vzájomne posunutých o trvanie ti.=> Ud [1(t) - 1(t- ti).

Podľa 2. Kirchhoffovho zákona:
 
Prvá časť riešenia popisuje tvar impulzu v čase od 0 po ti. - v intervale 0<=t<= ti., druhá časť vystihuje riešenie pre t> ti. Výsledný priebeh napätia uC(t) pre rôzne časové konštanty t =R1C1 je uvedený na obr. La11.

 
 
Obr. La10. 
Prístrojová realizácia obvodu z obr. La6

 

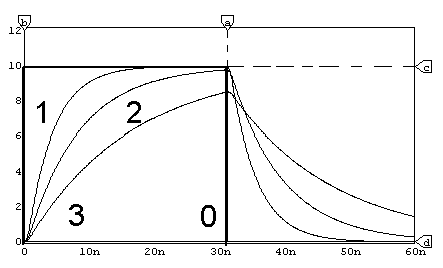
 Obr. La11. 
Časový priebeh napätia na kondenzátore uc(t) v integračnom RC článku pri rôznom pomere ti/t . Pri ( tI=30ns, C1=100pF) s R11=40W ; R12=80W ; R13=160W

Príklad 6 - Vplyv pracovného odporu na vlastnosti scintilačného detektora 
Určite priebeh napätia na výstupe obvodu z obr. La7 ako reakciu na scintilačný záblesk (F), charakterizovaný tvarom prúdového impulzu  Id.exp(-t/T) s amplitúdou Id a trvaním závislým od časovej konštanty záblesku T (obr. La12),  za predpokladu, že pred pôsobením impulzu bol kondenzátor vybitý a jeho napätie UC(t)=0.
 
 
Obr. La12. 
Tvar prúdového impulzu z výstupu scintilačného detektora id(t)=I.exp(-t/T) o trvaní svetelného záblesku určenom časovou konštantou T.

Podobne ako v predošlom príklade použijúc impulz Id.exp(-t/T) a jeho Laplacceov obraz 1/(p+1/T) bude podľa 1. Kirchhoffovho zákona:

 
Ilustrácia  závislosti (U/UCmax ) od  (T/R1C1) je na obrázoku  m4-b  F.