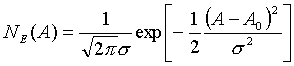|
|
|
Cieľom úvodnej úlohy praktika je oboznámenie sa so spôsobom detekcie ionizujúceho žiarenia, s vlastnosťami detektora ionizujúceho žiarenia ako aj so základnými metódami merania, ktoré sa používajú v experimentálnej jadrovej fyzike. K lepšiemu pochopeniu činnosti elektronickej aparatúry, ktorá spracováva signál z týchto detektorov by bolo potrebné poznať vlastnosti aj charakteristiky jednoduchších elektronických obvodov, z ktorých sa funkčné elektronické jednotky skladajú a poznať tiež definíciu základných pojmov z oblasti spektrometrie.
Elektronická aparatúra, ktorá umožňuje analyzovať amplitúdu impulzov z detektorov ionizujúceho žiarenia, ktorá sa používa vo väčšine úloh praktika je pomerne komplikovaná. Na rozdiel od úloh v predošlých základných praktikách (alebo úloh v ktorých sa verifikuje platnosť experimentov Stefana - Boltzmanna a Francka - Hertza v tomto praktiku), v ktorých bolo možné pomocou ampérmetrov a voltmetrov odmerať ustálené hodnoty príslušných prúdov a napätí, je pri meraní amplitúd impulzov (komplikovaného tvaru) situácia podstatne zložitejšia, pretože sa jedná vlastne o meranie prechodových javov (trvajúcich rádovo mikrosekunda). Takéto impulzy pri malých početnostiach by bolo možné napríklad fotografovať z obrazovky osciloskopu a následne analyzovať. Našťastie existujú aj iné pohodlnejšie metódy, ktoré možno použiť pri často sa vyskytujúcich udalostiach:
- Dokonalý spôsob používaný v mnohokanálových analyzátoroch používa najprv špeciálny vzorkovací obvod, pomocou ktorého sa meraným impulzom nabije vzorkovací kondenzátor a potom sa rýchlo odmerá napätie na tomto kondenzátore, napríklad pomocou analógovo - číslicového prevodníka.
- Prístrojovo menej kompilovaný spôsob, ktorý používame v tomto praktiku je založený na analyzovaní amplitúdy impulzu pomocou diskriminátorov. Pomocou diferenciálneho diskiminátora s automatickým posuvom diskriminačnej hladiny možno vytvoriť tzv. jednokanálový analyzátor (F), teda prístroj s obdobnými vlastnosťami ako mnohokanálový analyzátor len pomalšie pracujúci.
- rádioaktívneho rozpadu jadier (F);
- procesu interakcie žiarenia (častíc a fotónov) s médiom detektora (F) a tiež vplyv šumov aparatúry (F).
Cieľ úvodného praktika
Počas tohto úvodného praktika by ste teda mali:
- Zvoliť si vhodné trvanie jednotlivých meraní vzorky a pozadia s ohľadom na požadovanú presnosť merania. (F – Neistota nameranej hodnoty) - teda vedieť odpoveď na veľmi frekventovanú otázku z praktika : " Ako dlho to mám merať?"
- Oboznámiť sa s meracou aparatúrou, charakteristickou pre jadrovo-fyzikálne experimenty, ktorá je založená na meraní vlastností (amplitúdy a tvaru) elektrických impulzov, ktoré vznikajú v detektore po interakcii so žiarením (F A – experimentálne zariadenie, F B- Meranie so súpravou RFT 20046) - teda vedieť odpoveď na otázku : " Ako to mám merať?"
- Presvedčiť sa na základe merania o štatistickom charaktere registrovaných udalostí ( F úloha3-4 –Overenie štatistiky registrácie) - teda skutočne sa presvedčiť, že napriek tomu, že som nenameral číselne tú istú hodnotu ako môj kolega, tak môj výsledok môže byť rovnako správny, ak je v tolerancii neistoty merania.
| A-0 | Neistota nameranej hodnoty (chyby merania) |
Pri meraniach rádioaktívneho rozpadu (charakterizovaného rozpadovou konštantou l alebo polčasom rozpadu T1/2=ln2/l ) sa vyskytujú štatistické chyby. (Na základe predpisu MSA 0104-97 sa namiesto pojmu "chyba" zaviedol výraz "neistota".)
Štatistické neistoty rádioaktívneho
rozpadu sú
principiálne náhodné javy, popisované kvantovou mechanikou, v ktorých
možno
vypočítať pravdepodobnosť počtu rozpadov P(n) ako
funkciu
rozpadovej konštanty l
a doby merania t.
Štatistické neistoty rádioaktívneho rozpadu
Pre veľký celkový počet aktívnych atómov
n
a malú pravdepodobnosť rozpadu (lt<<1)
možno
použiť na charakterizovanie rozdelenia pravdepodobnosti počtu rozpadov
tzv. Poissonovo rozdelenie (F
obr. 3-3):
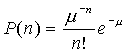 |
|
| v ktorom: | m=lt udáva stredný počet rozpadov za dobu t |
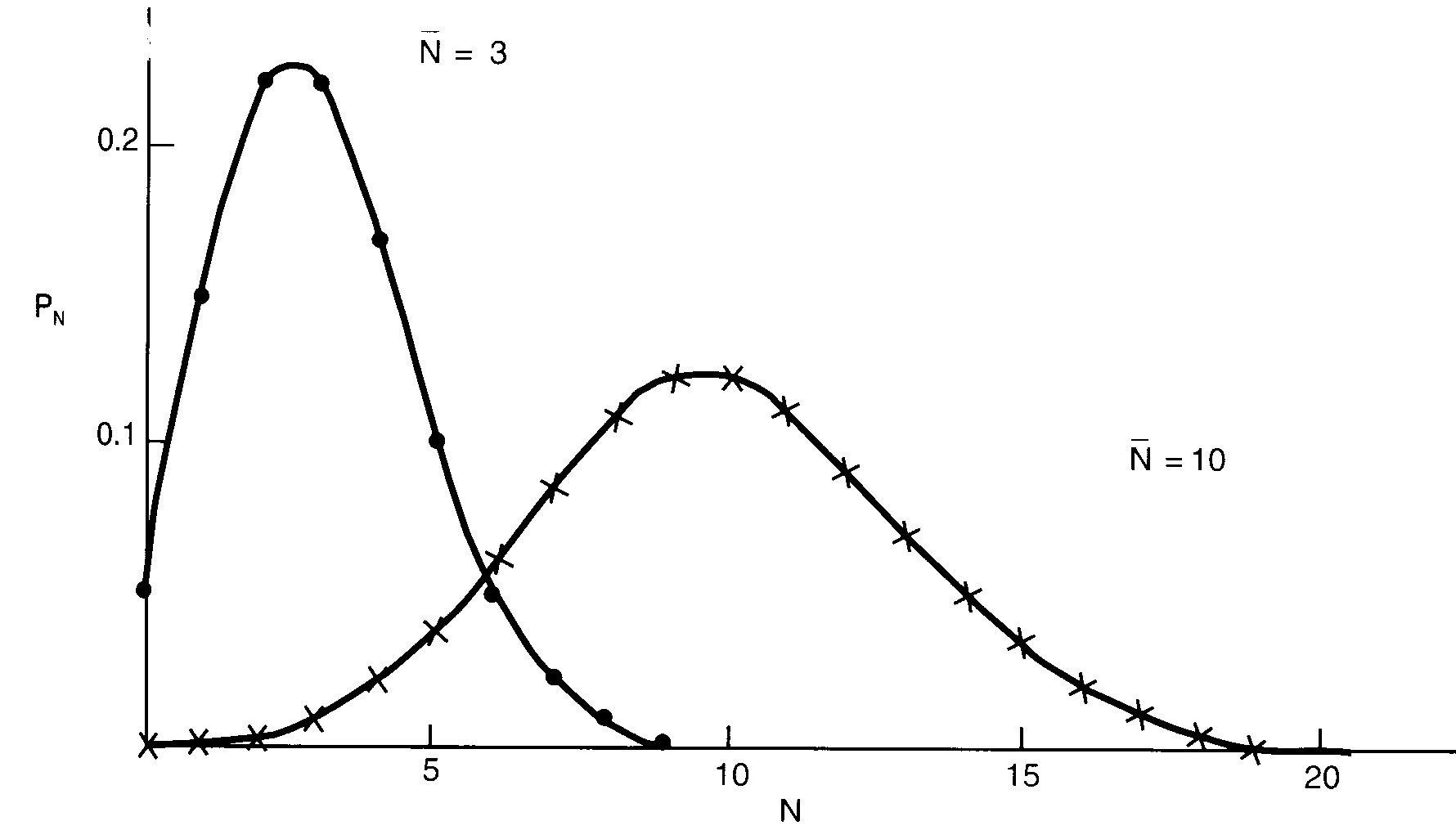 |
Obr. 3-3. Porovnanie Poissonovho rozdelenia pre strednú hodnotu N = 3 a N = 10. |
Pre prípad väčších hodnôt m
(m>10
až
15) možno aproximovať Poissonovo rozdelenie Gaussovým rozdelením (F
obr. 0-2) , ktoré charakterizuje rozdelenie náhodnej premennej n
v okolí strednej hodnoty m,
kde má Gaussova funkcia maximum.
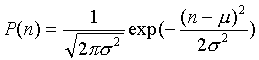 |
Rozlišovacia schopnosť detektora
Proces transformácie energie častice na amplitúdu impulzu má tiež pravdepodobnostný charakter. Jednotlivé etapy tohto procesu - ionizácia alebo vzbudenie, plynové zosilnenie v proporcionálnom počítači, zosilnenie primárneho elektrónového toku vo fotonásobiči - to je postupnosť interakcií častíc, ktoré sa podriaďujú pravdepodobnostným zákonom. Preto ak aj je energia detegovaných častíc rovnaká (presne monoenergetické častice), zodpovedajúce impulzy na výstupe detektora majú rôzne amplitúdy, t.j. amplitúdy sú rozdelené podľa určitého pravdepodobnostného zákona. Tvar amplitúdového rozdelenia sa často blíži k tvaru Gaussovho rozdelenia. Pravdepodobnosť NE(A) toho, že pri energii registrovanej častice E bude mať amplitúda impulzu na výstupe detektora hodnotu A .Toto rozdelenie má tvar píku so stredom pri A=A0, šírka píku je charakterizovaná parametrom s.
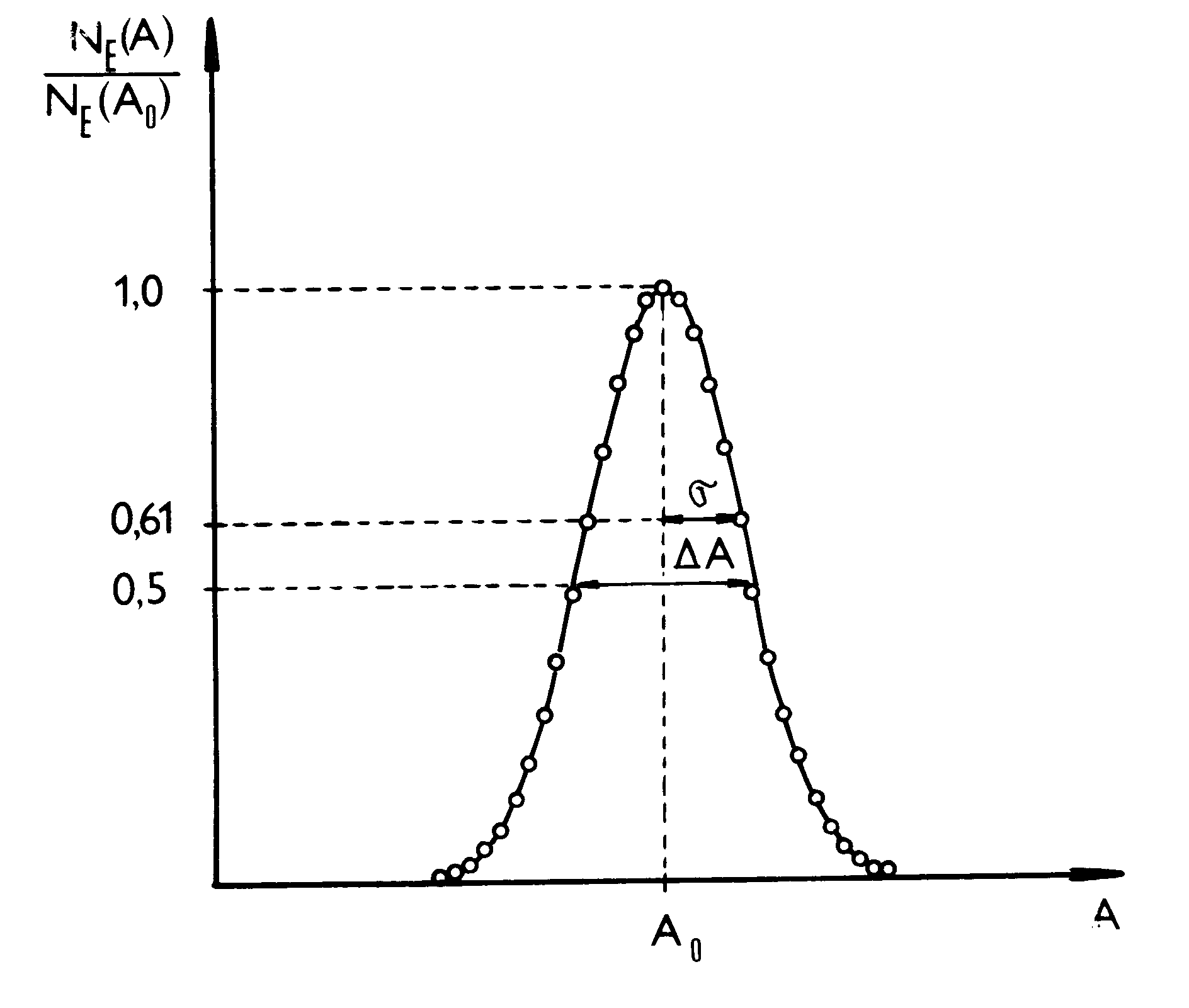 |
Obr.
0.2: Gaussovo rozdelenie
(s - stredná kvadratická odchýlka , DA - celková šírka píku meraná v polovičnej výške píku - FWHM )
|
Ak sú dve energie skúmaného žiarenia E1 a E2 natoľko blízko, že vzdialenosť medzi im odpovedajúcimi amplitúdovými píkmi A01 a A02 je podstatne menšia ako s, potom spektrometer s takýmto detektorom nemôže rozlíšiť (rozoznať) tieto energie.
V spektrometri sa ako miera rozlišovacej schopnosti detektora používa iná veličina - celková šírka píku FWHM=DA na úrovni polovičnej výšky maximálnej hodnoty rozdelenia.
Aby sme našli súvis medzi DA a s uvažujeme nasledovne. Maximum píku rozdelenia je pri amplitúde A=A0, tomu zodpovedá amplitúda rozdelenia NE (A0). Hľadáme také (A-A0), pre ktoré bude hodnota Gaussovho rozdelenia rovná polovici maximálnej hodnoty Gaussovho rozdelenia, t.j. NE(A)=(1/2)NE(A0). Po dosadení a úprave dostaneme (pozri obr. 0.2)
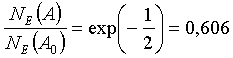 .
.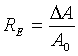
Vplyv šumu
Vplyvom šumu (fluktuácie šumových impulzov detektora charakterizovanú strednou kvadratickou odchýlkou sd a príspevoku vlastných šumov predzosilňovača a zosilňovača sz) sa zhorší energetická rozlišovacia schopnosť spektrometrického detektora - sst (pôvodne spôsobená následkom štatistického javu transformácie energie častice na amplitúdu impulzu v detektore pri interakcii žiarenia (častice alebo kvanta) s médiom detektora ). Tento výsledný efekt možno charakterizovať napr. pomocou strednej kvadratickej (štandardnej ) odchýlky fitovaného píku spektra scelk:
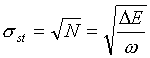 ,
,
Presnosť výsledku merania
1. Presnosť výsledku – vplyv predĺženia merania
Pri uvádzaní výsledku na
charakterizovanie
spoľahlivosti tohto výsledku uvádzame aj neistotu s.
Napríklad pre počet výskytov meranej udalosti N±sN
pripadajúcich na dobu merania t alebo počet udalostí za
jednotkový
interval - početnosť n= N/t±sn
je príslušná stredná kvadratická odchýlka:
| , resp. | 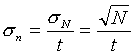 |
V praxi sa často nezajímame o absolútnu,
ale o
relatívnu (percentuálnu) neistotu výsledku danú pomerom:
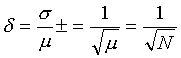 |
![]()
Príklad 1 na objasnenie pojmov
- Predpokladajme, že pri meraní rádioaktivity vzorky sa na displeji počítadla zobrazil údaj Na=100 impulzov. Potom je zaregistrovaný počet udalostí možno charakterizovať neistotou sNa=Na1/2=10 impulzov a údaj zapísať v tvare :
- Ak bol získaný údaj počtu impulzov Na, odmeraný za časový interval 1s je (Na = na a) početnosť:
- V prípade predĺženia doby merania na ta2 =100s by sme z tohto žiariča mohli zaregistrovať napr. Na2=10000 impulzov, čím by sme zmenšili relatívnu neistotu nameraného údaja:
- Ak by sme na základe údaja z bodu 3 (pri dobe merania na ta2 =100s a pri zaregistrovaní. Na2=10000 impulzov), určili početnosť:
|
|
udalostí |
Získaný počet udalostí Na bol teda odmeraný s relatívnou neistotou:
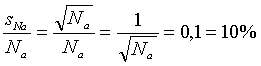 |
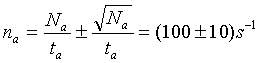 |
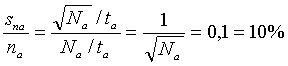 |
|
|
udalostí |
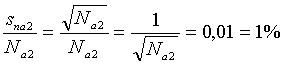 |
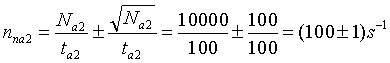 |
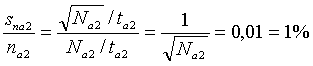 |
Uzáver, plynúci z príkladu 1:
Ak chceme zaregistrovať počet udalostí (impulzov) N s presnosťou okolo 1% je nutné predĺžiť trvanie merania (alebo použiť koncentrovanejšiu vzorku) tak, aby počet udalostí N~10000. Potom je
![]()
2. Presnosť výsledku – vplyv opakovaného merania
Často sa tiež vykonávajú opakované
merania tej
istej vzorky. Predpokladajme, pre jednoduchosť, že vzorka bola meraná
viackrát
(m - krát) na tom istom zariadení, v tých istých podmienkach a
vždy
sa registrovali impulzy za tú istú dobu merania. (Na takýto spôsob
merania
a charakterizovania neistôt merania ste boli zvyknutí z doterajších
praktík.)
Potom pre odhad strednej hodnoty platí
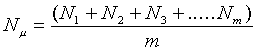 |
a pre neistotu (strednú kvadratickú
odchýlku)
tohto odhadu strednej hodnoty platí
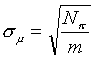 |
(Takto zadefinovaná neistota s je limitným prípadom, pre prípad nekonečného počtu meraní m. Pre bežnú prax (s konečným, väčšinou menším počtom členov m výberového súboru) sa používa odhad neistoty strednej hodnoty
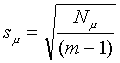 |
Presnosť merania možno teda zlepšiť jednak predĺžením trvania merania, alebo vykonaním viacnásobného počtu meraní.
![]()
Príklad 2 na objasnenie pojmov
Experimentálne si uvedený poznatok
môžete overiť
v praktiku. Ale teraz pre kontrolu ako zdroj údajov použijeme
namerané
hodnoty z tabuľky na obr. 3-8 (F
), odmerané v úlohe 3 - časť 4: Overenie štatistiky registrácie. Ako
zdroj
údajov pre príklad použijeme 10 hodnôt nameraných počtov udalostí Ni
z prvého stĺpca tabuľky (doplnené o neistoty si jednotlivých
meraní):
| Ni[s-1] |
39
|
44
|
38
|
49
|
56
|
51
|
34
|
28
|
45
|
33
|
| si[s-1] |
6.24
|
6.63
|
6.16
|
7.00
|
7.48
|
7.14
|
5.83
|
5.29
|
6.71
|
5.74
|
- Tieto počty udalostí Ni (v tomto prípade pri trvaní merania ti=1s sú číselne zhodné s početnostiami ni=Ni/ti±sI , a aj neistoty si početností sú číselne rovnaké ako neistoty jednotlivých meraní :
- Ak by sme iným počítadlom zaregistrovali za dobu t10=S ti.=10s počet udalostí N10=SNi=(36+44+38+49+56+51+34+28+45+33)=N10±(N10)1/2=(417±20,4) [1/10s] bude toto jednotlivé sumárne (10 sekundové) meranie počtu udalostí N10=SNI charakterizované neistotou s10=(N10)1/2=20,4 (10s)-1. V prípade ak chceme na základe tohto údaja určiť početnosť bude odhad strednej hodnoty početností:
- Ak chceme porovnať vplyv predĺženia trvania merania z bodu 2 s vykonaním viacnásobného počtu meraní môžeme pokladať m=10 hodnôt z tabuľky za opakované merania Ni tej istej vzorky a s pomocou nich odhadnúť strednú hodnotu (v danom prípade 1s trvania merania ide o strednú početnosť).
- Pre porovnanie: histogram Gaussovho rozdelenia na obr. 3.8 (F ) má stred píku (vlastne strednú hodnotu početnosti) n0=42,5± 6,5 s-1. Túto hodnotu n0, získanú na základe m=300 údajov, môžeme pre naše porovnávanie pokladať za hodnotu najspoľahlivejšie vystihujúcu strednú hodnotu početnosti. (Uvedená hodnota s =6,5 s-1 však necharakterizuje neistotu určenia strednej početnosti n0 na základe 300 údajov, ale charakterizuje neistotu jednotlivého opakovaného merania Ni.)
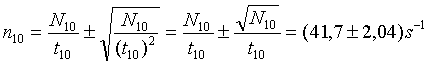 |
určený s neistotou s10=(N10/t102)1/2=(N10)1/2/t10=20,42/10=2,04
s-1. Teda neistota tohto merania bude menšia ako
neistota
jednotlivého merania Ni , vykonaného za dobu 1s v
bode
1..
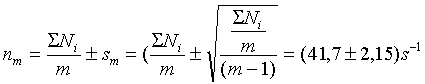 |
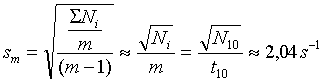 ). ). |
Štatistika nám teda hovorí len s akou pravdepodobnosťou je daný typ voľby spoľahlivosti správny:
- na základe odseku b) vidno, že toto meranie za dlhší časový interval je presnejšie ako namerané početnosti v tabuľke z bodu a), lebo neistota odhadu početnosti na základe dlhšieho merania s10=(N10/t102)1/2=(N10)1/2/t=2,04 s-1 je menšia ako neistoty jednotlivých meraní početností (napr. s5=7,48 s-1 pri N5 v tabuľke);
- na základe odseku c) vidno, že neistota odhadu početnosti pri opakovanom meraní sm={S Ni/[m(m-1)]}1/2= 2,15 s-1 je obdobná ako v odseku b) a teda je menšia ako sú neistoty jednotlivých meraní (napr. s5=7,48s-1 pri N5 v tabuľke);
- na základe s daného Gaussovho rozdelenia spomínaného v odseku d) môžeme tvrdiť, že odhad výskytu udalostí:
- na úrovni štandardnej odchýlky s (v intervale <T0-s , T0+s >) je správny v 68,3% prípadov. (To, že v malom súbore hodnôt z odseku a) až 4 hodnoty (N5=56, N6=51, N8=28, N10=33, t.j. 40% údajov) sú mimo uvedený interval a jedna hodnota (N4=49) je na hranici intervalu <36, 49> odhadu na úrovni štandardnej odchýlky len demonštruje, že ide o aplikovanie štatistiky na súbor s malým počtom údajov);
- na úrovni 2 štandardných odchyliek s (v intervale <T0-2s , T0+2s >) je správny v 95% prípadoch;
- na úrovni 3 štandardných odchyliek s (v intervale <T0-3s , T0+3s >) je správny v 99,75% prípadoch;
-
![]()
3. Vplyv pozadia
Pri meraní rádioaktívneho žiarenia, kde pozadie Np je relatívne veľké sa odlišuje počet zaregistrovaných udalostí N (impulzov) od počtu impulzov od vzorky Nv :
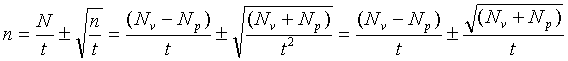 |
Aké poučenie pre praktikum plynie teda z vyššie uvedeného? Pri nezamyslení sa nad problémom sa nám môže stať, že vykonáme meranie vzorky a pozadia „rýchlo“ za rovnaký interval s menšou presnosťou, tak ako ilustruje nasledujúci ilustračný príklad 3 a 4.
![]()
Ilustračný príklad 3 – početnosť bez pozadia
Pri odmeraní počtu impulzov N=1000 za
interval
t=100s je odhad strednej hodnoty početnosti (tohto jediného merania, s
príslušnou neistotou odhadu):
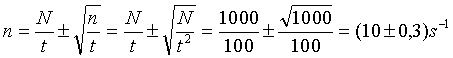 . . |
Teda presnosť výsledku charakterizuje relatívna neistota 3%.
![]()
Ilustračný príklad 4 – početnosť za prítomnosti pozadia
Pri odmeraní počtu impulzov od vzorky Nv=1000
za
interval t=100s odmeraný za prítomnosti pozadia (Np=100
za interval t=10000s) je odhad strednej hodnoty početnosti od vzorky
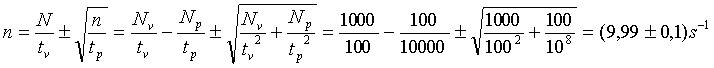 |
Vďaka predĺženému trvaniu merania pozadia pozadie už prakticky nevplýva na presnosť výsledku. (Presnosť výsledku charakterizuje relatívna neistota 1%. Pre porovnanie pri použití rovnakého trvania merania pre pozadie a vzorku t=100s by bol výsledok n=9,99± 1,1 s-1 - teda oveľa menej dôveryhodnejší. Presnosť tohto výsledku charakterizuje relatívna neistota 11%.)
![]()
Ilustračný príklad 5 – viacnásobné opakovanie merania
Pri viacnásobnom odmeraní tej istej početnosti impulzov za interval t=1s sme získali hodnoty n1=620, n2=627, n3=622. Potom výsledný odhad strednej hodnoty početnosti (za interval t=1s) je
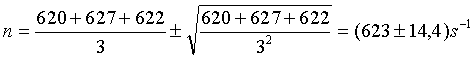 |
Teda presnosť výsledku charakterizuje relatívna neistota 2,3%.
![]()
| A | Experimentálne zariadenie |
| B | Súprava RFT 20046 |
| C |
|
V prvej časti (pri ručnom ovládaní diskriminačnej hladiny):
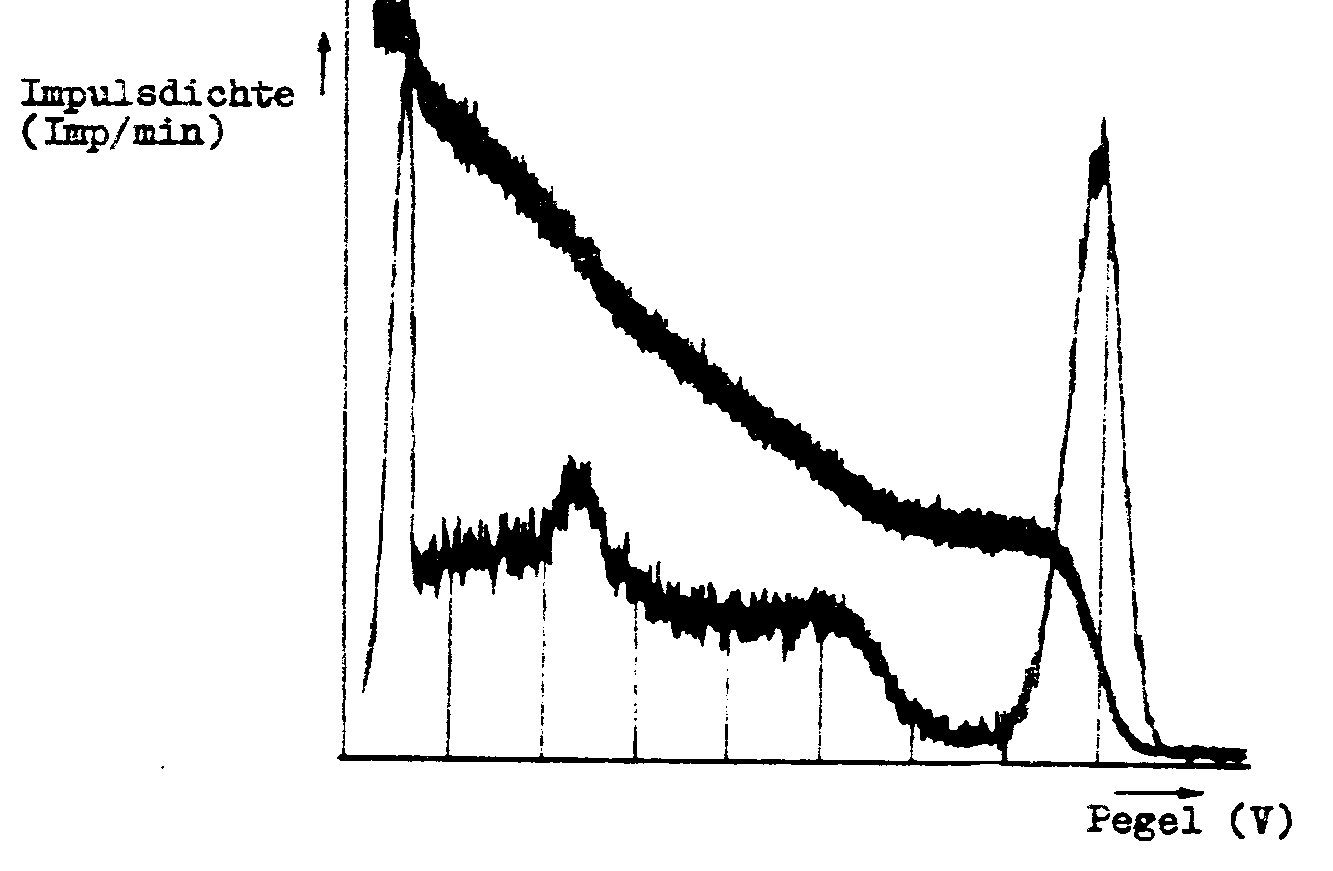
- Odmerajte integrálne a diferenciálne spektrum doporučeného žiariča pri vhodnom napätí na detektore Uvn a vhodnom zosilnení na súprave RFT 20046 s ručným posuvom diskriminačnej hladiny (podľa doporučenia vedúceho praktika). Nakreslite grafy s obidvoma spektrami (Výsledok by sa mohol podobať na obrázok 3.2).
- Experimentálne si overte, že predĺženie trvania merania alebo zopakovanie meraní zvyšuje presnosť merania, resp. zmenšuje neistotu nameraného údaja. Vykonajte preto nasledujúce merania:
- Odmerajte počet zaregistrovaných udalostí Nv (počtu impulzov) za interval t=100s a určite neistotu výsledku (absolútnu svN a relatívnu svN/Nv) a vypočítajte početnosť nv=Nv/t ±svn podobne ako v demopríklade 1.
- Vykonajte 10 opakovaných meraní Ni o trvaní ti=10s a a určite neistotu (absolútnu si a relatívnu si/Ni) jednotlivých meraní ako aj odhad strednej početnosti (1/s) na základe týchto opakovaných meraní - podobne ako v demopríklade 2.
- Odmerajte počet zaregistrovaných udalostí Nv (počtu impulzov) za interval t=10s. Vykonajte meranie pozadia (počtu impulzov Np) za interval tp=100s a interval tp=10s a určite skutočný počet udalostí N=(Nv-Np) ±(Nv+Np)1/2 a po prepočítaní na jednotku času (1/s) aj početnosť spôsobenú žiarením zo vzorky n=N/t± (n/t )1/2 - podobne ako v demopríklade 3 a 4.
- Porovnajte získané výsledky početností bez prítomnosti pozadia, získané v bode c, pri rôznych trvaniach merania pozadia a vyberte najpresnejší spôsob merania s najmenšou neistotou výsledku.
- Pomocou voľby 1 programu úlohy 5 (F ) odmerajte integrálne a diferenciálne spektrum doporučeného žiariča pri nastavenej dolnej diskriminačnej hladine Udd = 0,2 V (aby prípadné šumy v dôsledku automatického nastavovania mierky v zobrazení nezmenšovali zbytočne obrázok), pri vhodnom napätí na detektore Uvn a vhodnom zosilnení na súprave RFT 20046 (Podľa možnosti použite rovnaké napätie na detektore Uvn a rovnaké zosilnenie na súprave RFT 20046 ako pri predošlom meraní s ručným ovládaním diskriminačnej hladiny). Vytlačte spoločný graf s obidvoma spektrami.
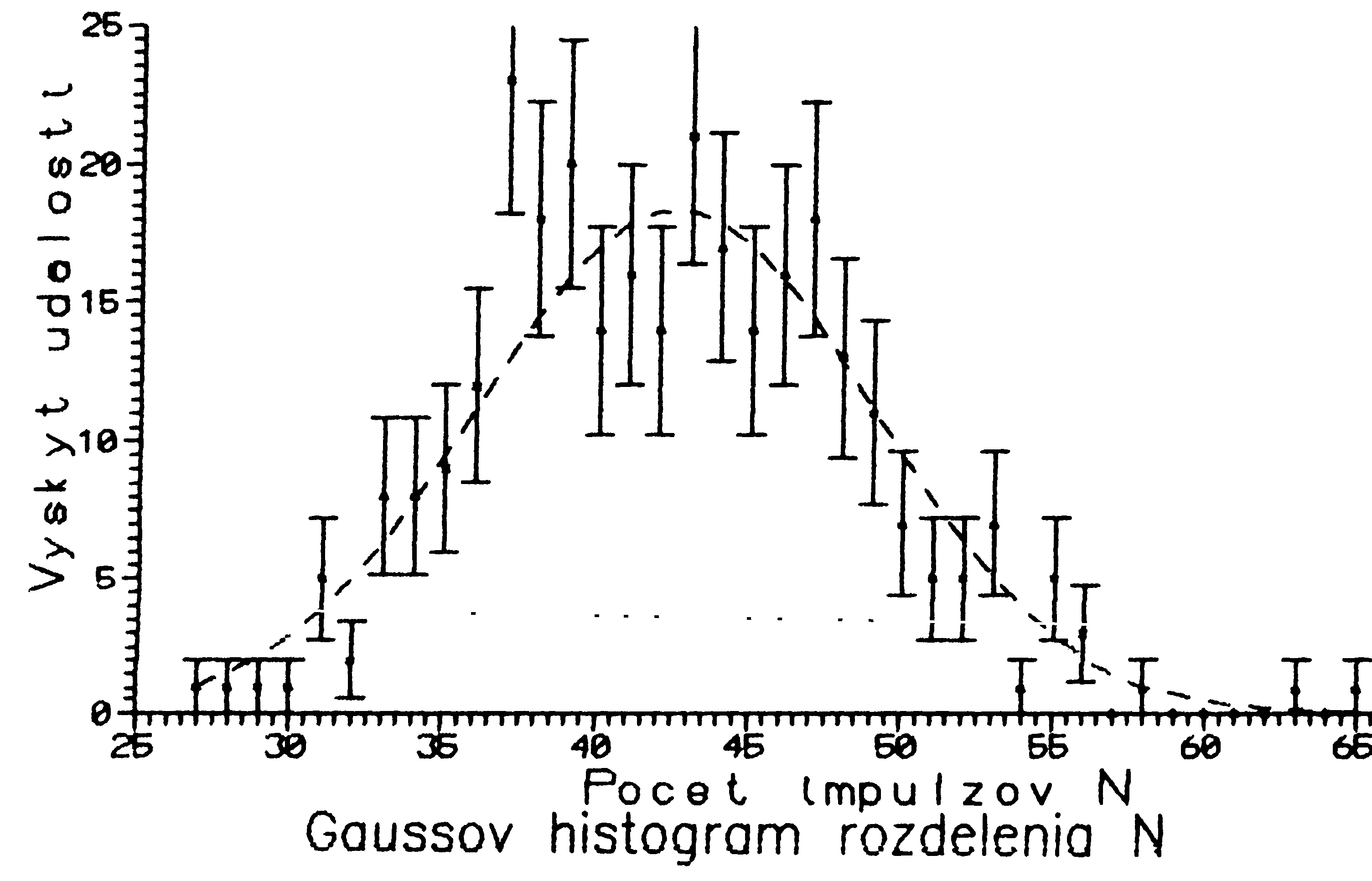
- Pomocou voľby 4 programu úlohy 3 (F ) odmerajte histogram štatistiky registrácie udalostí s použitím žiariča z predchádzajúcej úlohy pri vhodnom napätí Uvn a zosilnení súpravy tak, aby počet registrovaných udalostí za sekundu nepresiahol 100.´Na záver merania vytlačte dáta z merania prvých 100 udalostí histogramu a výpočtom sa presvedčte, či dostanete podobné parametre Gaussovho rozdelenia udalostí ako vytlačil počítač. Potom pokračujte v meraní a sledujte ako sa ďalej menia parametre histogramu (poloha stredu píku rozdelenia T0 a stredná kvadratická odchýlka s ). Porovnajte výsledky merania početnosti nv=Nv/t ±svn získané v úlohe 2a) s parametrami histogramu To ±s . Na preloženie fitovacej krivky Gaussovho rozdelenia z nameraných hodnôt použi vzťah (F )
 |
|
|
V druhej časti (pri
automatizovanom
posuve diskriminačnej hladiny):
 |
 |
| Obr.3-8. Príklad nameraného rozdelenia registrovaných udalostí. (histogram Gaussovho rozdelenia so stredom píku 42,5 ± 6,5 a plochou pod píkom 300 ±17). Uvedené dáta predstavujú náhodnú vzorku 100 z posledne odmeraných 300 hodnôt, ktoré slúžia na kontrolu. |
|
|
|
|