|
|
|
Cieľ úlohy:
Oboznámiť sa s jednoduchým scintilačným spektrometrom a s jeho
použitím na určenie energie gama prechodov a aktivity nuklidov
emitujúcich gama žiarenie.
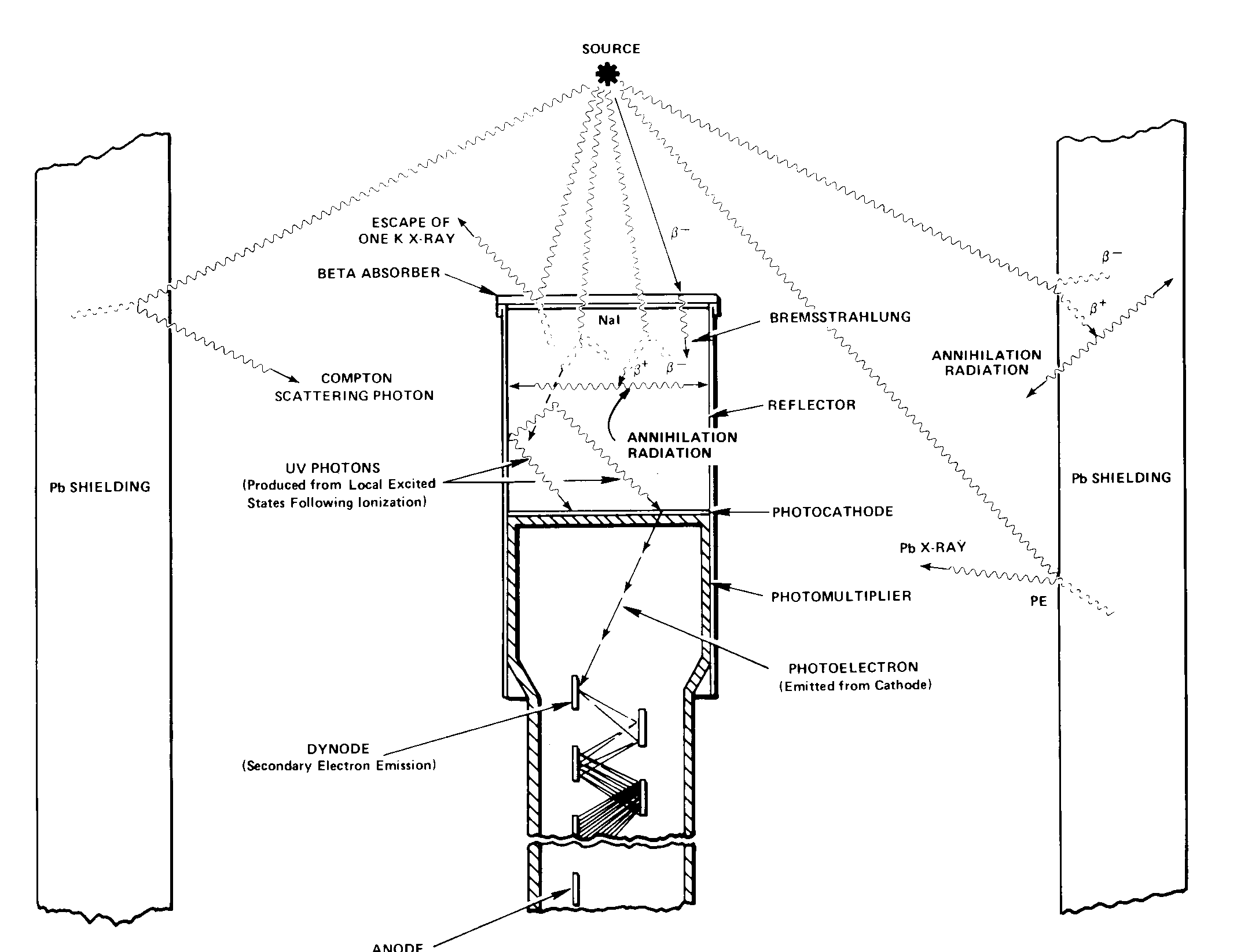 |
| Obr. 15-1 ilustujúci procesy prebiehajúce pri detekcii gama žiaenia pomocou scintilačného detektora s kryštálom NaI(Tl). |
![]()
Jadro, ktoré sa nachádza v rozličných stavoch, má rozdielnu energiu. Stav s najnižšou energiou sa nazýva základný stav. Všetky ostatné stavy sú vzbudené. Spektrum vzbudených stavov je diskrétne., t.j. jadro môže byť len na istých energetických úrovniach.
Všetky vzbudené stavy sú nestabilné. Prechod jadra zo vzbudeného stavu do stavu s nižšou energiou je možný dvoma spôsobmi: emisiou gama kvanta, alebo odovzdaním energie vzbudenia jednému z elektrónov v obale., ktorý opustí atóm. Prvý proces sa nazýva gama prechod, druhý vnútorná konverzia.
Energia gama kvanta, emitovaného pri gama prechode, je daná rozdielom energetických hladín , medzi ktorými nastal prechod. Jednou z možností určenia energie gama kvánt je použitie scintilačného spektrometra s jedným kryštálom. V najjednoduchšom prípade sa v takomto spektrometri impulzy z fotonásobiča, zosilnené lineárnym zosilňovačom, privádzajú na jednokanálový amplitúdový analyzátor. Tento prepustí len impulzy, ktorých amplitúda zodpovedá nastavenej úrovni kanálu. Tieto impulzy registruje počítacie zariadenie. Impulzy, ktorých amplitúda je väčšia, alebo menšia ako hladiny vytvárajúce kanál, sa neregistrujú. Sledovaním početnosti impulzov v závislosti od ich amplitúdy (t.j. úrovne kanálu amplitúdového analyzátora) získavame amplitúdové spektrum žiarenia.
Pre spektrometriu je dôležité, aby úmernosť medzi amplitúdami impulzov a energiou detekovaných kvánt bola lineárna. Táto požiadavka sa obvykle spĺňa v širokom intervale energií pre rôzne scintilátory. Ďalším kritériom pri výbere scintilátora pre spektrometriu je jeho absorpčná schopnosť pre gama žiarenie a účinnosť premeny energie kvánt, absorbovaných v scintilátore, na energiu svetelných fotónov. V tomto smere má najlepšie vlastnosti kryštál jodidu sodného aktivovaný táliom. Pre absorpciu gama žiarenia je dôležité pomerne vysoké atómové číslo jódu (Z=53).
Treba poznamenať, že prístrojové spektrum (amplitúdové
rozdelenie impulzov) je vlastne spektrum sekundárnych elektrónov,
produkovaných pri interakcii gama žiarenia s látkou scintilátora. Pri
tejto interakcii si konkurujú tri procesy (fotoefekt, Comptonov
rozptyl, tvorba párov). To sa prejavuje v pomerne zložitom tvare
spektra aj monoenergetického gama žiarenia, ktoré odpovedá jadru s
jediným vzbudeným stavom. Na obr. 15.2 je rozpadová schéma 137Cs
a prístrojové spektrum jeho gama žiarenia.
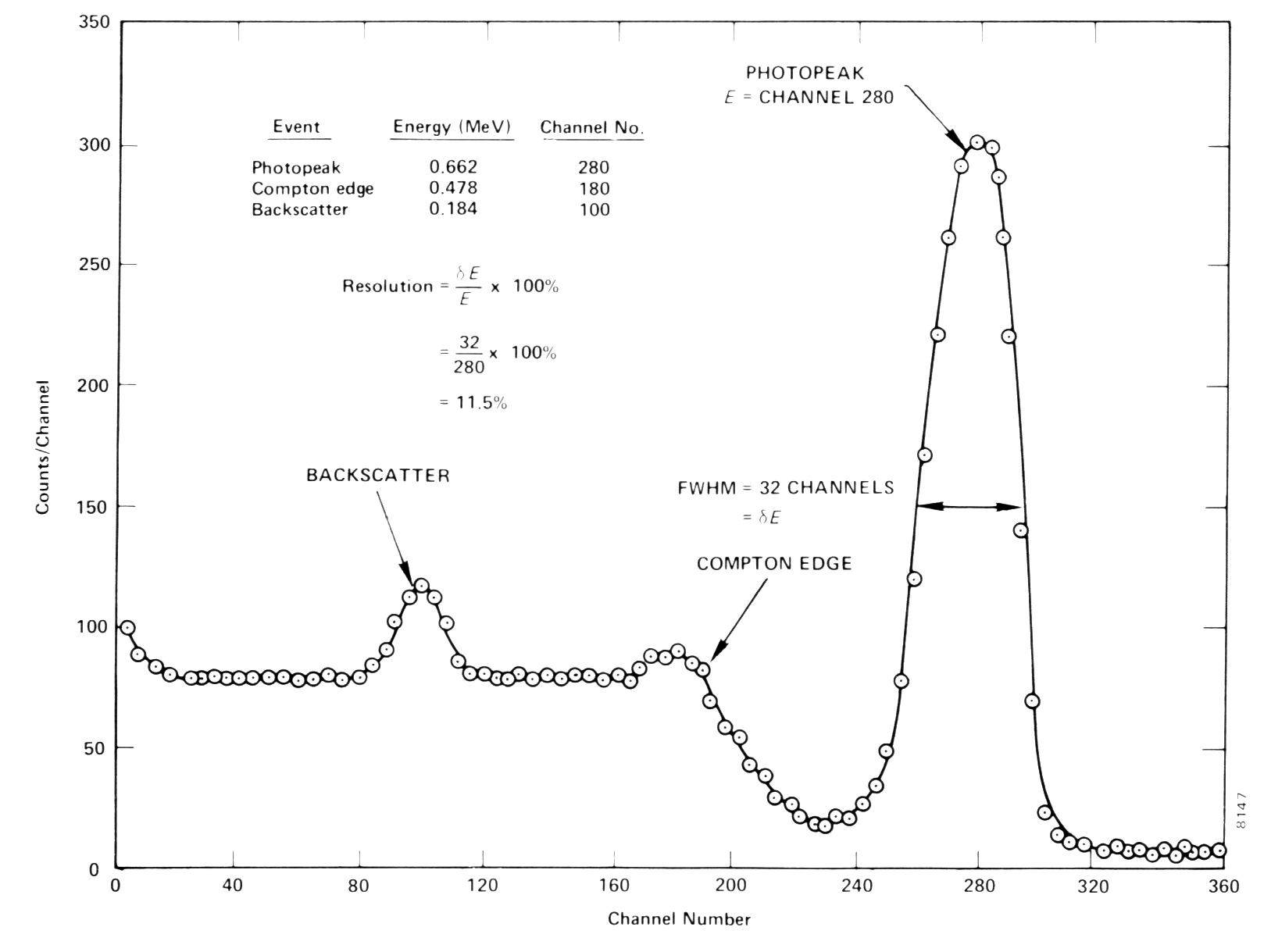 |
| Obr.15.2 ilustrujúci fotoefekt (pík úplnej absorpcie), Comptonov rozptyl (pík spätného rozptylu (Backscatter) a Comptonovskú hranu (Comptonedge)) a rozlíšenie FWHM. |
Pík na konci amplitúdového rozdelenia zodpovedá úplnej absorpcii energie gama kvánt v scintilátore a nazýva sa pík úplnej absorpcie. Prispieva k nemu fotoefekt a mnohonásobný rozptyl. Pík má tvar Gaussovho rozdelenia
Comptonovsky rozptýlené kvantá prispievajú do spojitej časti spektra. V scintilátore sa absorbuje v tomto prípade len energia odrazených elektrónov (majú energiu od 0 po Emax) a sekundárne gama kvantum z kryštálu uniká. Toto spojité rozdelenie je charakteristické málo výrazným maximom v oblasti hraničnej energie (Comptonova hrana).
V oblasti nižších energií sa v spektre na spojitom rozdelení objavuje široký nesymetrický pík, spôsobený spätným rozptylom žiarenia z okienka fotonásobiča a púzdra kryštálu. Nazýva sa preto pík spätného rozptylu.
Ak je energia kvánt väčšia ako 2m0c2 = 1,022 MeV, uplatňuje sa aj tvorba párov, pri ktorej vznikajú ako dôsledok anihilácie pozitrónu dve kvantá s energiou 0,511 MeV. Únik jedného alebo obidvoch týchto kvánt zapríčiňuje vznik ďalších píkov (jednoduchého a dvojitého úniku).
Zdrojom parazitného žiarenia je žiarenie, vznikajúce pri
interakcii gama kvánt v okolitom materiáli (rtg. žiarenie, anihilačné
kvantá).
|
|
|
|
![]()
Experimentálna časť.
Z amplitúdového rozdelenia môžeme priamo určiť amplitúdu (číslo kanálu), odpovedajúcu polohe píku úplnej absorpcie. Táto poloha v škále amplitúd alebo kanálov je mierou energie absorbovaných kvánt. Prechod od polohy píku, určenej číslom kanálu, ktorému odpovedá jeho maximum, k polohe píku v škále energií, vyžaduje poznať vzťah medzi energiou kvánt a polohou píku (amplitúdou impulzov). Tento vzťah udáva kalibračná krivka. K jej zostrojeniu treba poznať aspoň dva body, ktorými táto priamka prechádza. Nájdeme ich meraním amplitúdového rozdelenia žiaričov, ktoré emitujú kvantá známej energie. Výhodou je, ak žiarič, ktorý pre tieto ciele používame, emituje len kvantá jednej energie (monoenergetické žiarenie). Orientácia v jeho spektre je potom jednoduchá. Nájdeme polohu píku V a zostrojíme priamkovú závislosť E=E(V)
Tomuto postupu hovoríme energerická kalibrácia. Jej výsledkom
je kalibračná priamka E=E(V). Umožňuje priradiť energiu píkom v spektre
žiarenia ďalších rádionuklidov.
Identifikácia rádoinuklidov.
Podľa energie emitovaného gama žiarenia sa dá identifikovať rádionuklid, ktorý je jeho zdrojom. Väčšina rádionuklidov emituje pri svojom rozpade kvantá viacerých energií. V spektre je potom niekoľko píkov. Určíme ich polohy a pomocou kalibračnej priamky vypočítame energie kvánt. Pomocou tabuliek gama prechodov identifikujeme nuklid.
Všeobecne je k tomu treba mať niektoré ďalšie informácie.
Napríklad okruh žiaričov prichádzajúcich do úvahy, prirodzene
rádioaktívne nuklidy, nuklidy vznikajúce pri štiepení uránu, žiarič zo
skupiny dodávaných etalónov a pod. Doplňujúcou informáciou je tiež
znalosť polčasu rozpadu. Tieto informácie obvykle sú k dispozícii a
vyplývajú zo znalosti pôvodu meranej vzorky.
Analýza spektra 137Cs.
Amplitúdové spektrum gama žiarenia získavame ako spektrum
elektrónov, vyprodukovaných v interakciách gama kvánt s atómami
scintilátora. Ak kvantum s energiou Eg interaguje
fotoefektom, získava fotoelektrón energiu
| Ef = Eg – EVK |
EVK je väzbová energia elektrónu na K vrstve v atóme. Atóm, v ktorom chýba elektrón na K vrstve, nie je stabilný. Voľné miesto zaplní elektrón z vyšších vrstiev, pričom sa vyžiari energia rovná EVK vo forme rtg. kvanta. Ak sa toto kvantum absorbuje v kryštále, celá energia Eg sa odovzdá v scintilátore a vznikajúci impulz sa zaregistruje v píku úplnej absorpcie.
Pri Comptonovom efekte sa energia kvanta Eg rozdelí
medzi odrazený elektrón a rozptýlené kvantum. Energia tohoto
sekundárneho kvanta sa dá vypočítať, ak vychádzame z predstavy pružnej
zrážky kvanta s voľným elektrónom. Pre energiu kvanta Eg' rozptýleného
o uhol q dostaneme
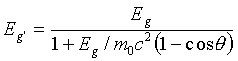 |
Ak je q =180o, t.j.
kvantum je rozptýlené naspäť, bude jeho energia
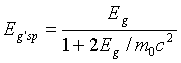 |
|
|
Pri uhle q< 180o bude energia rozptýleného kvanta väčšia a energia odrazených elektrónov menšia.
Maximálna hodnota energie elektrónov Emax odpovedá
preto spätnému rozptylu kvanta. Pretože vždy platí, že energia
odrazeného elektrónu je
| Ee = Eg – Eg' |
Môžeme určiť energiu prislúchajúcu comptonovej hrane ako
| (15.2) |
pričom energia Eg' sp je daná vzťahom (15.1).
![]()
|
|
|
|
Energetické rozlíšenie.
Píky, ktoré majú blízke energie, spektrometer nedokáže
rozlíšiť, v spektre dostaneme jeden zložený pík. Energetické rozlíšenie
charakterizuje schopnosť prístroja rozlíšiť takéto dva píky. Analogicky
k iným spektrálnym prístrojom sa definuje ako šírka čiary v polovičnej
výške maxima píku DE. To znamená, že píky
vzdialené o viac ako D E budú v spektre
rozlíšené. V opačnom prípade dostaneme jeden zložený pík. Obvykle sa
udáva relatívna hodnota rozlíšenia v %, t.j.
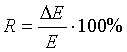 , , |
(15.3) |
| R - | je energetické rozlíšenie | |
| D E - | je šírka v polovičnej výške maxima píku a | |
| E - | je poloha píku úplnej absorpcie. |
Za predpokladu, že kalibračná priamka prechádza počiatkom, možno do vzťahu (15.3) dosadiť za DE šírku v počte kanálov a za E polohu píku v kanáloch. Ak priamka počiatkom neprechádza, dostali by sme pri takomto počítaní chybný výsledok. Musíme preto šírku píku i polohu píku určiť v energetickej škále, použitím kalibračnej priamky.
Energetické rozlíšenie spektrometra závisí na energii, je preto dôležité uviesť energiu, pre ktorú je určené. Zaužívané je udávať ho pre energiu kvánt emitovaných 137Cs (662 keV).
![]()
|
|
|
|
Určenie aktivity gama žiaričov.
Plocha píku úplnej absorpcie je úmerná počtu kvánt emitovaných žiaričov. Sú dva spôsoby ako určiť aktivitu rádionuklidu pomocou jeho gama žiarenia. Prvý spočíva v porovnaní počtu impulzov zaregistrovaných v píku pri meraní žiariča, ktorého aktivitu určujeme a etalónu, ktorého aktivitu poznáme. Táto metóda je analogická relatívnej metóde stanovenia aktivity meraním beta žiarenia. Početnosti impulzov aj tu korigujeme na pozadie. Prakticky to znamená, že od početnosti impulzov pod píkom ( súčet počtu impulzov v kanáloch, ktoré sú v hraniciach píku ) odpočítame počet impulzov zaregistrovaných v hraniciach píku bez žiariča.
Etalón musí spĺňať podmienky rovnakej geometrie merania a rovnakej energie kvánt so žiaričom, ktorého aktivitu určujeme.
Druhá metóda využíva znalosť účinnosti detekcie kvánt v píku úplnej absorpcie (píková účinnosť) ef, určenej pomocou etalónov emitujúcich kvantá iných energií. Nevyžaduje teda etalón meraného nuklidu a v tomto zmysle je „absolutnou" metódou. Píková účinnosť je funkciou energie a geometrie žiarič – detektor. Zostrojenie tejto závislosti vyžaduje preto niekoľko etalónov s rôznymi energiami emitovaných kvánt.
Touto metódou sa aktivita žiariča A určí podľa vzťahu
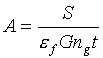 |
(15.4) |
Kde:
|
S -
|
počet impulzov pod píkom |
|
ef -
|
píková účinnosť |
|
G -
|
geometrický faktor |
|
ng -
|
počet kvánt pripadajúcich na jeden rozpad |
|
t -
|
doba merania v jednotlivých kanáloch |
Ak je bodový žiarič na osi válcového scintilátora vo vzdialenasti h, faktor G = plocha čela scintilátora/4ph2.
![]()
Počet impulzov v píku (plocha píku) S je korigovaný na pozadie. Pík,
ktorého plochu určujeme, môže byť superponovaný na spojitom rozdelení. V
tomto prípade pozadie nemôžeme jednoducho namerať ako počet impulzov
bez vzorky, ale musíme poznať charakter spojitého rozdelenia pod píkom a
toto rozdelenie dopočítať. Exaktne riešiť túto úlohu je ťažko.
Predpokladáme preto, že pozadie pod píkom sa dá aproximovať priamkou
(obr. 15.3).
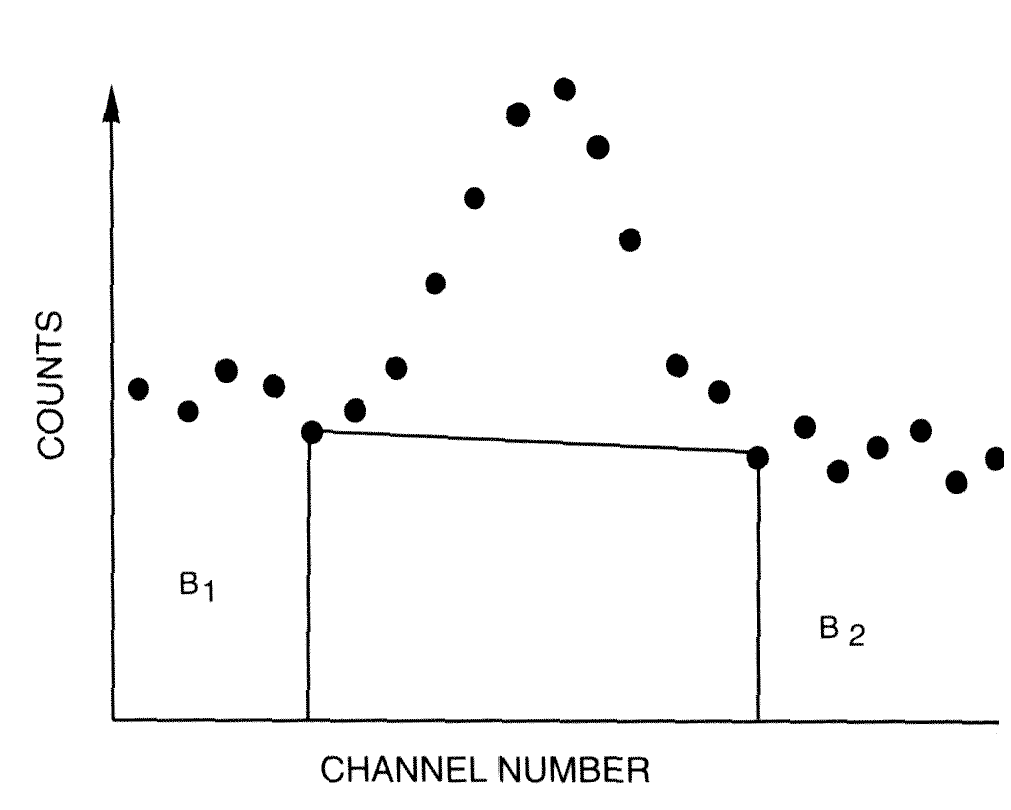 |
Obr. 15.3 Plocha pod píkom A = P-(n/2)*(B1+B2), ktorá vznikne po odpočítaní lichobežníka reprezentujúceho pozadie (o stranách B1, B2 a výške n = počet kanálov medzi B1 a B2) od celkovej plochy P, reprezentuje počet zaregistrovaných udalostí, ktoré chceme vyhodnotiť. [Odchylky označenia na obrázku a v texte: B1=Ni, B2=Nj a channel number =(j-i+1)] |
Plocha píku, ktorého hranice sú i,j a im odpovedajúce
početnosti sú Ni a Nj sa určí podľa vzťahu
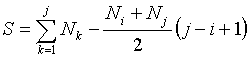 |
(15.5) |
Pozadie (druhý člen na pravej strane) sa nahrádza plochou lichobežníka. Táto metóda výpočtu pozadia pod píkom sa volá lichobežníková metóda.
Pri výpočte chyby s(A) na obrázku
15.3 je nedostatočné použiť vzťah pre chybu rozdielu (A - P). Treba
uvažovať, že plocha bola odmeraná nepriamo pomocou počtov udalostí v
jednotlivých kanáloch N1, N2, ...Nn, takže pre takto odmeranú plochu A
= f(N1,N2,.. Nn) je:
|
|
|
|
|
|
| kde: P1, P2 ..Pn sú údaje v kanáloch po odpočítaní pozadia, pričom SPi = P. |
Nasledujúce spektrá ilustrujú interakciu gama žiarenia s látkou scintilátora:
- spojitú oblasť spektra v oblasti nižšich energii, spôsobenú rozptylom kvant gama na orbitálnych elektrónoch v atóme (Comptónov jav),
- pík úplnej absorbcie (fotopík, ktorý vzniká interakciou gama kvánt s atómami scintilátora),
- resp. pík, ktorý vzniká pri tvorbe párov elektrón-pozitrón (pri energii gama kvant väčšej ako 2*0,511Mev=1,022Mev)
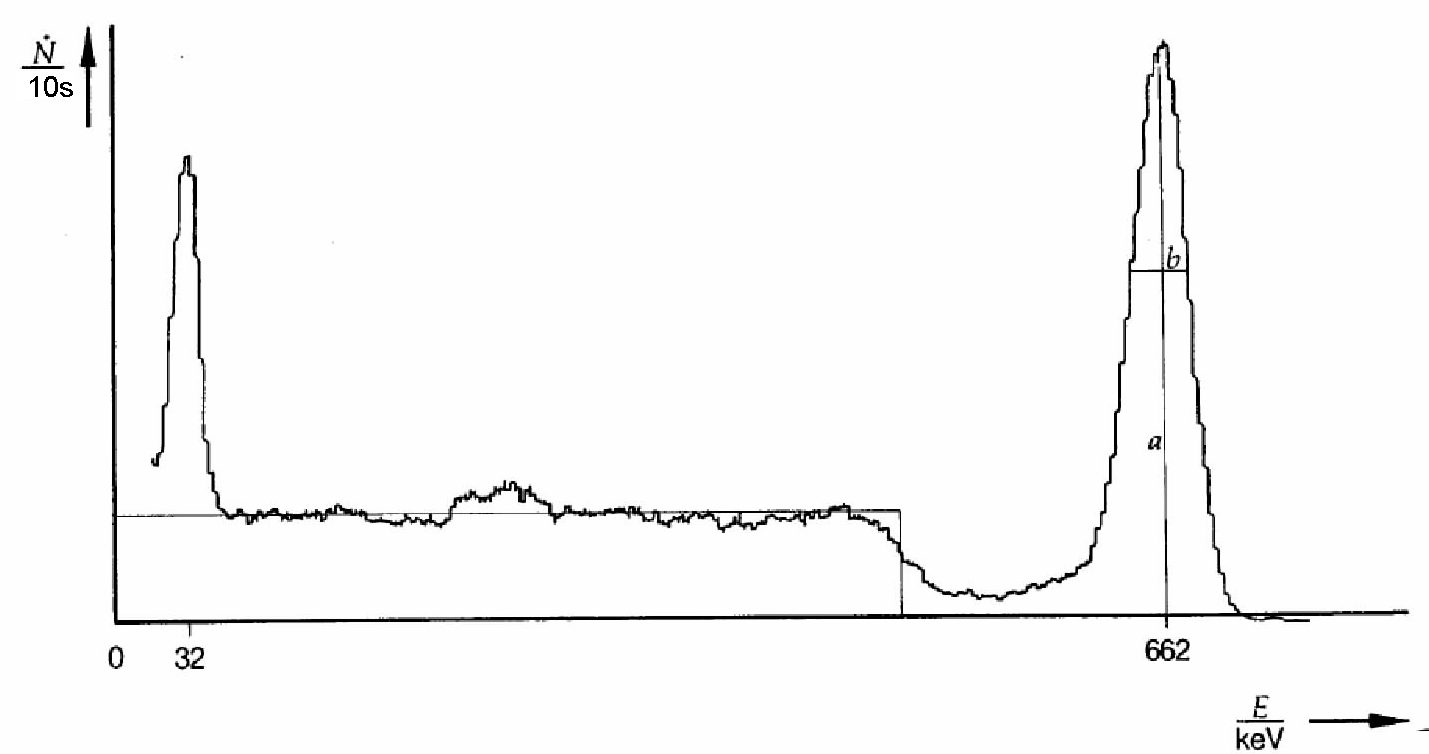 |
Obr. 15.3a Ilustračné spektrum žiariča 137Cs. a-poloha píku, b-energetické rozlíšenie. |
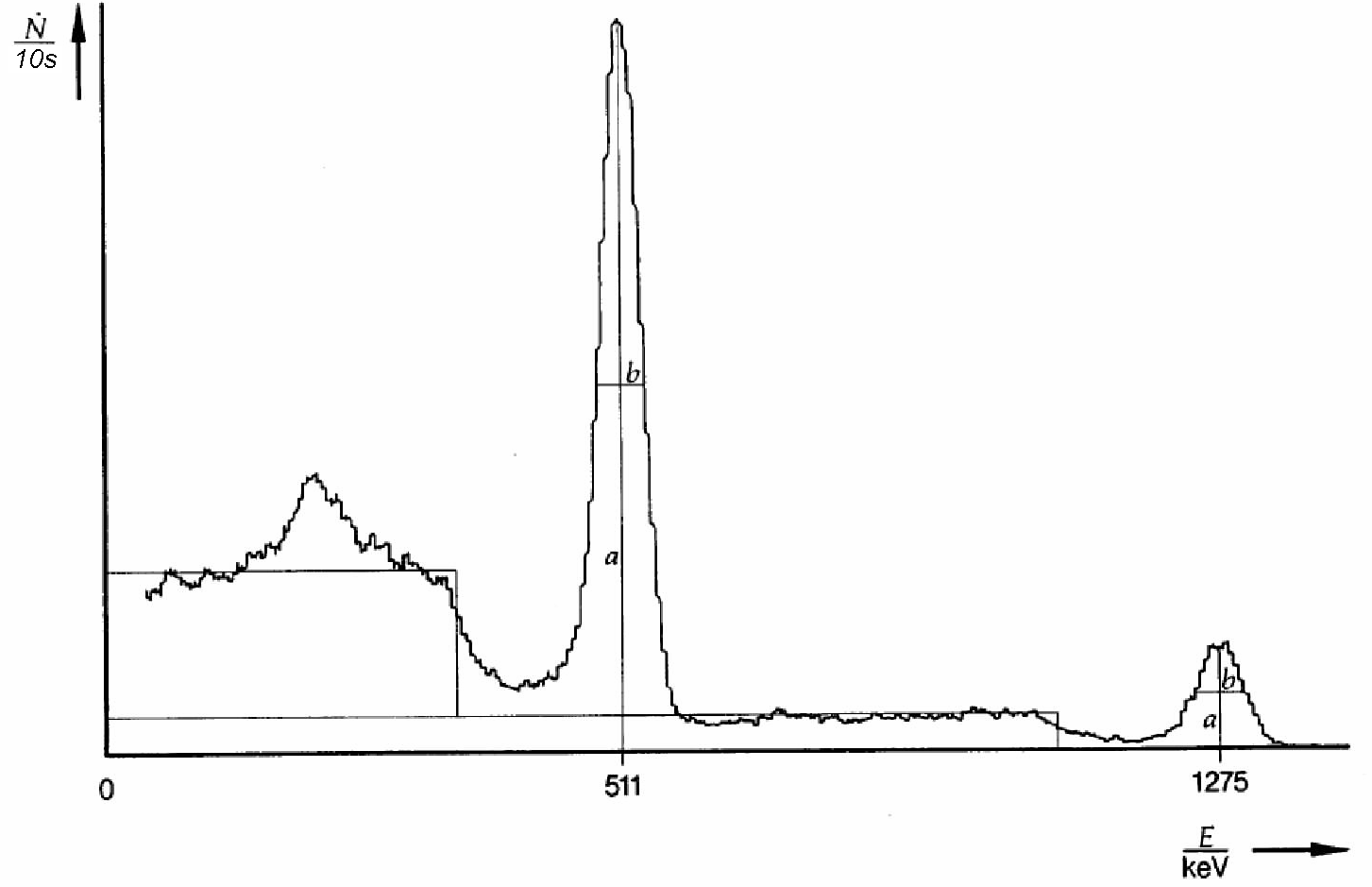 |
Obr. 15.3b Ilustračné spektrum žiariča 22Na.
a-poloha píku, b-energetické rozlíšenie. |
![]()
|
|
|
|
Pracovné úlohy:
Urobiť energetickú kalibráciu spektrometra.
- Určiť energie prislúchajúce píkom neznámeho žiariča a identifikovať ho.
- Určiť energiu Comptonovej hrany a píku spätného rozptylu v spektre 137Cs a porovnať ich s vypočítanými hodnotami.
- Určiť energetické rozlíšenie spektrometra.
- Určiť aktivitu nuklidu, ktorý sme identifikovali v úlohe 2.
Postup merania.
Zmenou zosilnenia alebo napätia na fotonásobiči dosiahneme, aby pík úplnej absorpcie 137Cs bol asi v 100 kanále amplitúdového analyzátora. Spektrometer okalibrujeme pomocou niekoľkých žiaričov známej energie kvánt (tab. 15.1). Nameriame celé amplitúdové rozdelenie neznámeho žiariča a píky spektier etalónových žiaričov. Neznámy žiarič by mal byť vzdialený od čela scintilátora ~10 cm (pravdepodobne však v podmienkach praktika to nebude splnené). Určíme polohy známych píkov, na základe kalibračnej priamky určíme ich energiu, určíme energie píkov neznámeho žiariča a pomocou tab. 15.1 ho identifikujeme. Jeho aktivitu vypočítame podľa vzťahu (15.4), plochy píkov pritom určujeme podľa vzťahu (15.5). Vyhodnotenie meraní Vám uľahčí program k úlohe 15.
Energie píku spätného rozptylu a comptonovej hrany v spektre "neznámeho žiariča" vypočítame podľa vzťahov (15.1 a 2) a porovnáme ich s energiami, určenými z nameraného spektra tohoto nuklidu.
![]()
Tabuľka 15.1 Energie gama prechodov.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Energetické rozlíšenie spektrometra určíme pre pík 137Cs.
Ak kalibračná priamka neprechádza počiatkom, dosadíme D E aj E v MeV. Výsledky merania spracujeme
graficky, s vyznačením údajov týkajúcich sa píkov a comptonovej hrany
"neznámeho žiariča".
|
|
|
|