Logické funkcie

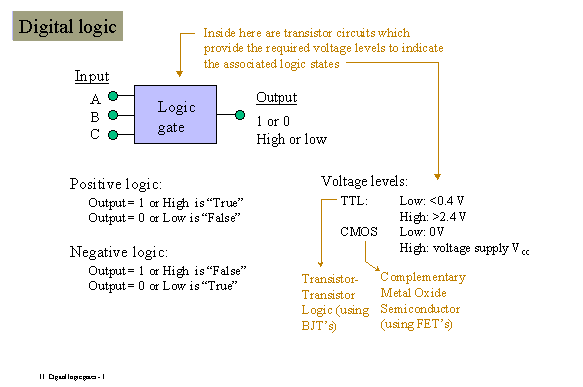
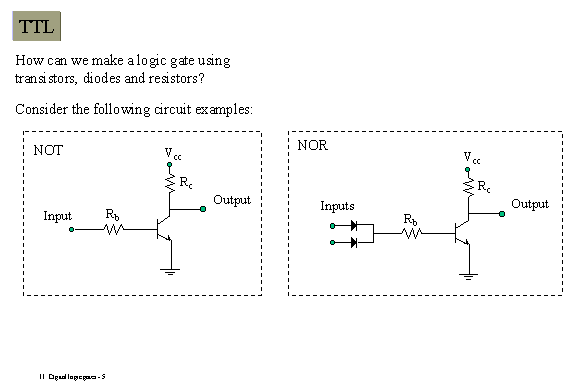Logická (dvojková) premená je veličina x, ktorá môže nadobúdať len dve hodnoty - označené 0 a 1 a nemôže sa meniť spojite. Pri realizácii logických funkcii pomocou fyzikálnej štruktúry sa priraďujú dvojkové stavy 1 a 0 fyzikálnym stavom vysoká logická úroveň High (H) a nízka logická úroveň Low (L). Logická konvencia priradenia úrovne može byť:  kladná - keď pravdivému tvrdeniu - stavu 1 zodnovedá vysoká napäťová úroveň H a nepravdivému tvrdeniu - stavu 0 zodpovedá nízka napäťová úroveň L, záporná - keď pravdivému tvrdeniu - stavu 1 zodnovedá nízka napäťová úroveň L a nepravdivému tvrdeniu - stavu 0 zodpovedá vysoká napäťová úroveň H. 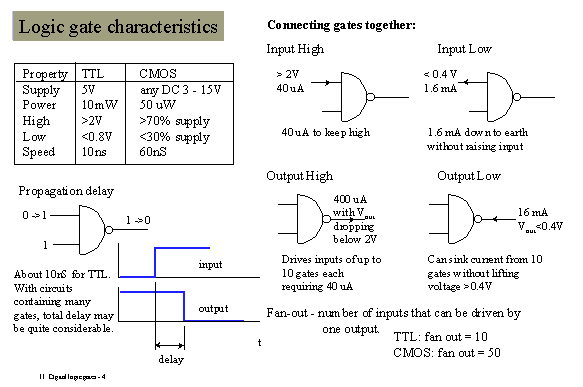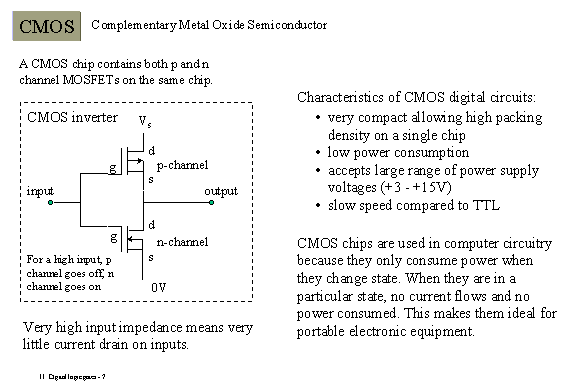Konkrétne hodnoty napätia, ktoré zodpovedajú úrovniam H a L závisia od realizácie fyzikálnej štruktúry TTL, CMOS a pod. 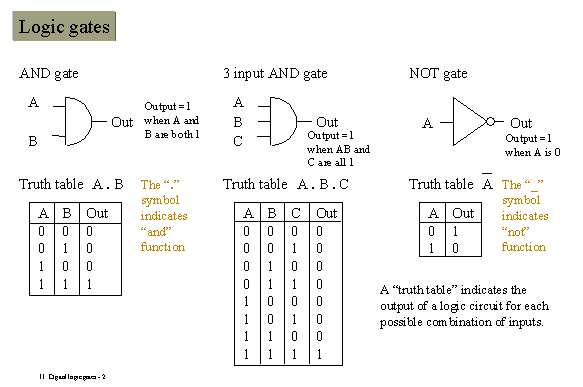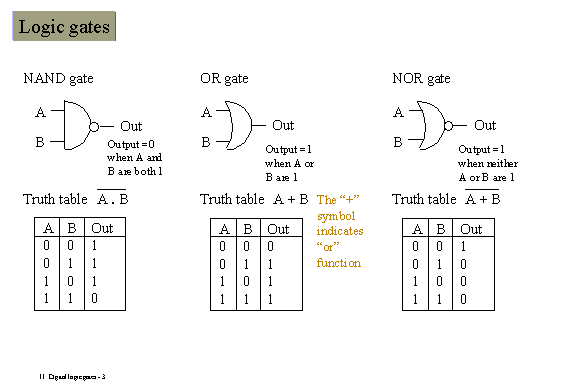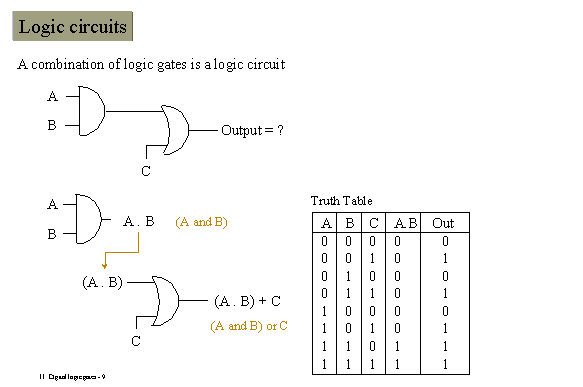Logický alebo číslicový obvod sa nazýva kombinačný, ak stav premenej na jeho výstupe závisí len od kombinácie vstupných premených a nie od ich predchádzajúceho nastavenia.

 

Logický súčin - hradlo AND

Najjednoduchší spôsob na charakterizovanie funkcie logických hradiel umožňuje pravdivostná tabuľka logickej funkcie.  AND - hradlo na realizovanie funkcie logického súčinu (prienik, konjukcia) NOT - hradlo na realizovanie negácie alebo inverzie (krúžok v schématickej značke hradla)

 

Rôzne možnosti realizovania logickej funkcie

OR - hradlo na realizovanie logického súčtu (zjednotenie, disjunkcia), NOR - negovaný logický súčet, NAND - negovaný logický súčin. Obrázok ilustruje rôzne možnosti na realizáciu určitej logickej funkcie. V praxi sa na realizovanie logických funkciii používajú logické členy NAND a NOR.

Základné parametre logických členov

Základným dynamickým parametrom integrovaného logického člena (TTL, CMOS) je rýchlosť zmeny amplitúdy výstupnej odozvy, ktorá sa charakterizuje prenosovým oneskorením (propagation delay). Amplitúda zodpovedajúca stavom H a L sa môže nachádzať v určitom rozmedzí amplitúd. Z hľadiska spojovania logických členov je dôležité výstupné vetvenie N (fun-out number), ktoré udáva počet jednotkových vstupov ďalšich členov, ktoré možno pripojiť na výstup.

Možnosť realizácie logickej funkcie pomocou tranzistorov a diód

Obrázok ilustruje príklad použitia tranzistorov a diód na realizáciu jednoduchej logickej funkcie.

Možnosť použitia unipolárnych tranzistorov MOSFET

Unipolárne tranzistory MOS (predovšetkým tranzistory MOSFET - ovládané elektrickým poľom pomocou hradla, ktoré je odizolované od polovodiča izolátorom SI02) umožňujú vysokú integráciu prvkov v integrovanom obvode. Prednosťou použitia MOSFET je nízka spotreba.

 

Možnosť použitia unipolárnych tranzistorov CMOS

V logických obvodoch, v ktorých operačná rýchlosť nie je prvoradá (rýchlosť CMOS je nižšia v v porovnaní s TTL) a dôležitejšia je malá spotreba našli široké uplatnenie komplementárne tranzistory typu NMOS a PMOS - skátene CMOS. Napríklad invertor CMOS na obrázku pozostáva len z dvoch komplementárnych tranzistorov. Napájacie napätia CMOS môžu byť v rozsahu 3 - 15V. Pri napájacom napätí 5V sú logické úrovne CMOS prakticky kompatibilné s úrovňami obvodov TTL

 

Integrované prevedenie 74XXX

Čo do počtu a rozmanitostí typov sú najrozšírenejšie integrované logické členy s tranzistorovo - tranzistorovými väzbami - TTL.Obrázok ilustruje príklady integrovaného prevedenia rodiny členov 74XXX.

 

Príklad realizovania jednoduchej logickej funkcie

Obrázok ako príklad ilustruje realizovaniejednoduchej logickej funkcie, zadanej pravdivostnou tabuľkou.

 

Boolova algebra

Pomocou postulátov pre základné logické funkcie (AND, OR, NOT) je odvodená skupina zákonov, ktoré tvoria základ metódy úprav a zjednodušovania logických výrazov. Napríklad výrazy pre komutatívnosť logického súčtu a súčinu, asociatívnosť logického súčtu a súčinu a distributívnosť logického súčtu vzhľadom k súčinu sú analogické zákonom klasickej algebry. Zákon vyjadrujúci distributívnosť logického súčtu vzhľadom k súčinu nemá však svoj ekvivalent v klasickej algebre. Z hľadiska použitia pri zjednodušovaní zložitejšich logických výrazov je zaujímavý de Morganov zákon. (Umožňuje zjednodušiť praktickú realizáciu logických zapojení len na základe obvodov NAND a NOR. ) .

 

Príklad 1 realizovania Boolovej logickej funkcie

Obrázok ilustruje príklad obvodovej realizácie logickej funkcie na základe symboliky algeraického zápisu.

 

Príklad 2 realizovania Boolovej logickej funkcie

Obrázok ilustruje príklad postupu pri obvodovej realizácie logickej funkcie..

 
 

Neekvivalencia - exluzivne OR

V praxi sa na realizáciu logických funkcii najčastejšie používajú ako univerzálne kombinačné články logické členy NAND a NOR. Pomocou týchto členov možno zostaviť aj ďalší základný obvod XOR - člen neekvivalencie, vykonávajúci funkciu súčtu vo význame vylučovacom (XOR má aj svoju špeciálnu symbolickú značku)

 

Analýza logických obvodov

Pred vlastnou realizáciou logickej funkcie pomocou integrovaných logických obvodov často možno pomocou zákonov Boolovej algebry zjednodušiť výsledný algebraický výraz a tým aj obvodovú realizáciu. Existuje niekoľko metód na analýzu logických výrazov - najznámejšia je grafická metóda Karnaughových máp.

 

Binárna sčítačka

Binárna sčítačka je príkladom aritmetického (číslicového a nie logického) kombinačného obvodu. Polovičná sčítačka (Half adder) pre 1 bit na obrázku pozostáva z obvodu XOR a obvdu AND. V obvode XOR sa vyhodnocuje bit A a bit B vytvára sa čiastočný súčet Sum. V obvode AND sa zisťuje stav keď je bit A=1 a bit B=1, pri ktorom dochádza k prenosu Carry. Pri sčítaní viacbitových čisel je treba uvážiť aj prenos z predchádzajúcich rádov, čo umožňuje obvod úplnej sčítačky pre 1 bit (Full adder)